Full-Length SAT Math Practice Test-Answers and Explanations

Did you take the SAT Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
The Absolute Best Book to Ace the SAT Math Test
SAT Math Practice Test Answers and Explanations
Section 1 – No Calculator
1- Choice B is correct
\((-5m^2+4m-2)+(3m^2-3)\), Add like terms together: \(-5m^2+3m^2\)
\(4m\) doesn’t have like terms. \((-2)+(-3)=-5\), Combine these terms into one expression to find the answer: \(-2m^2+4m-5\)
2- Choice D is correct
Method 1: Plugin the values of \(x\) and \(y\) provided in the options into both equations.
A. \((4,2)→3x-y=6→3(4)-(2)≠6\)
B. \((2,4)→3x-y=6→3(2)-(4)≠6\)
C. \((2,-3)→ 3x-y=6→3(2)-(-3)≠6\)
D. \((2,0) → 3x-y=6→3(2)-(0)=6\)
Only option D is correct.
Method 2: Multiplying each side of \(3x-y=6\) by 2 gives \(6x-2y=12\) Then, adding the corresponding side of \(6x-2y=12\) and \(x+2y=2\) gives \(7x=14\). Dividing each side of \(7x=14\) by 7 gives \(x=2\). Finally, substituting 2 for \(x\) in \(x+2y=2\), or \(y=0\). Therefore, the solution to the given system of equations is \((2,0)\).
3- Choice D is correct
If \(f(x)=2x+4(2-x)+4\), then find \(f(-2x)\) by substituting \(-2x\) for every \(x\) in the function. This gives: \(f(-2x)=2(-2x)+4(2-(-2x))+4\),
It simplifies to: \(f(-2x)=-4x+8+8x+4=4x+12\)
4- Choice D is correct
First, find the equation of the line. All lines through the origin are of the form \(y=mx\), so the equation is \(y=-\frac{3}{5}x\). Of the given choices, only choice C \((\frac{4}{3},-\frac{4}{5})\), satisfies this equation:
\(y=-\frac{3}{5}x→3=-\frac{3}{5}(\frac{4}{3})=-\frac{4}{5}\)
5- Choice A is correct
Add 8 both sides of the equation \(18x-7=25\) gives \(18x=25+7=32\).
Dividing each side of the equation \(18x=32\) by 18 gives \(x=2\). Substituting 2 for \(x\) in the expression \(10x-12\) gives \(10(2)-12=8\).
6- Choice D is correct
The input value is \(-3\). Then: \(x=-3\), \(f(x)=2x^2-2x+1→ f(-3)=2(-3)^2-2(-3)+1=18+6+1=25\)
7- Choice B is correct
To rewrite \(\frac{1}{\frac{1}{x-2}\frac{1}{x+3}}\) , first simplify \(\frac{1}{x-2}+\frac{1}{x+3}\).
\(\frac{1}{x-2}+\frac{1}{x+3}=\frac{1(x+3)}{(x-2)(x+3)}+\frac{1(x-2)}{(x+3)(x-2)}=\frac{(x+3)+(x-2)}{(x+3)(x-2)}\)
Then: \(\frac{1}{\frac{1}{x-2}\frac{1}{x+3}}=\frac{1}{\frac{(x+3)+(x-2)}{(x+3)(x-2)}}=\frac{(x-2)(x+3)}{(x-2)+(x+3)}\) (Remember, \(\frac{1}{\frac{1}{f}}=f\))
This result is equivalent to the expression in choice B.
8- Choice A is correct
Since \((1, 2)\) is a solution to the system of inequalities, substituting 1 for \(x\) and 2 for y in the given system must result in two true inequalities. After this substitution, \(y < a+x\) becomes \(2 < a+1\), or \(a>1\) and \(y > x+b\) becomes \(2 > 1+b\) or \(b<1\). Therefore, \(a>b\).
9- Choice C is correct
First find the slope of the line using the slope formula. \(m=\frac{y_2-y_1}{x_2-x_1 }\)
Substituting in the known information. \((x_1, y_1 )=(1,6), (x_2, y_2 )=(-3,2)\)
\(m=\frac{2-6}{-3-1}=\frac{-1}{-1}=1\), Now the slope to find the equation of the line passing through these points. \(y=mx+b\), Choose one of the points and plug in the values of \(x\) and \(y\) in the equation to solve for \(b\). Let’s choose point \((-3, 2)\). Then: \(y=mx+b→2=(-3)+b→5=b→b=5\), The equation of the line is: \(y=x+5\)
Now, plug in the points provided in the choices into the equation of the line.
A. \((-8,-2) →y=x+5→-2=(-8)+5→-2=-3\) This is NOT true.
B. \((-2,-5) → y=x+5→-5=(-2)+5→-5=3\) This is NOT true.
C. \((-8,-3) →y=x+5→-3=(-8)+5→-3=-3\) This is true.
D. \((6,-6) → y=x+5→6=(-6)+5→6=-1\) This is NOT true!
Therefore, the only point from the choices that lie on the line is \((-8,-3)\).
10- Choice A is correct
You can find the possible values of \(a\) and \(b\) in \((ax+2)(bx-3)\) by using the given equation \(a+b=6\) and finding another equation that relates the variables \(a\) and \(b\). Since \((ax+2)(bx-3)=8x^2-cx-6\), expand the left side of the equation to obtain \(abx^2+2bx-3ax-6=8x^2-cx-6\)
Since \(ab\) is the coefficient of \(x^2\) on the left side of the equation and 8 is the coefficient of \(x^2\) on the right side of the equation, it must be true that \(ab=8\)
The coefficient of \(x\) on the left side is \(2b-3a\) and the coefficient of \(x\) in the right side is \(-c\). Then: \(2b-3a=-c\), \(a+b=6\), then: \(a=6-b\)
Now, plug in the value of \(a\) in the equation \(ab=8\).
Then: \(ab=8→(6-b)b=8→6b-b^2=8\)
Add \(-6b+b^2\) both sides. Then: \(b^2-6b+8=0\)
Solve for \(b\) using the factoring method. \(b^2-6b+8=0→(b-2)(b-4)=0\)
Thus, either \(b=2\) and \(a = 4\), or \(b = 4\) and \(a = 2\). If \(b = 2\) and \(a = 4\), then
\(2b-3a=-c→2(2)-3(4)=-c→c=8\), If \(b= 4\) and \(a = 2\), then
\(2b-3a=-c→2(4)-3(2)=-c→c=-2\), Therefore, the two possible values for \(c\) are \(8\) and \(-2\).
11- Choice A is correct
In order to figure out what the equation of the graph is, first find the vertex. From the graph, we can determine that the vertex is at \((2,-6)\). We can use vertex form to solve the equation of this graph. Recall vertex form, \(y=a(x-h)^2+k\), where \(h\) is the \(x\) coordinate of the vertex, and \(k\) is the \(y\) coordinate of the vertex. Plugging in our values, you get \(y=a(x-2)^2-6\)
To solve for \(a\), we need to pick a point on the graph and plug it into the equation.
Let’s pick \((0,-2)\), \(-2=a(0-2)^2-6→ -2=a(-2)^2-6→ -2=4a-6\)
\(4=4a→a=1\)→Now the equation is: \(y=(x-2)^2-6\), Let’s expand this,
\(y=(x^2-4x+4)-6, y=x^2-4x-2\), The equation in Choice C is the same.
12- Choice A is correct
Multiplying each side of \(\frac{8}{3x}=\frac{4}{(x-5}\).
\(8(x-5)=12(x)⇒ 8x-40=12x ⇒ 4x=-40⇒x=-10\), Therefore, the value of \(\frac{3x}{5}=\frac{3(-10)}{5}=-6\).
13- Choice B is correct
The equation of a circle can be written as \((x-h)^2+(y-k)^2=r^2\)
where \((h, k)\) are the coordinates of the center of the circle and \(r\) is the radius of the circle. Since the coordinates of the center of the circle are \((1,-3)\), the equation is \((x-1)^2+(y+3)^2=r^2\), where \(r\) is the radius. The radius of the circle is the distance from the center \((1,-3)\), to the given endpoint of a radius, \((5,2)\). By the distance formula, \(r^2=(5-1)^2+(2+3)^2=16+25=41\),
Therefore, an equation of the given circle is \((x-1)^2+(y+3)^2=41\)
14- Choice D is correct
To solve for \(cosA\) first identify what is known.
The question states that ∆ABC is a right triangle whose \(n∠B=90^\circ\) and \(sinC=\frac{3}{5}\).
It is important to recall that any triangle has a sum of interior angles that equals 180 degrees. Therefore, to calculate \(cosA\) use the complementary angles identify of a trigonometric function. \(cosA=cos(90-C)\),Then: \(cosA = sinC\)
For complementary angles, the \(sin\) of one angle is equal to the \(cos\) of the other angle. \(cosA=\frac{3}{5}\)
15- Choice D is correct
To solve this problem, first recall the equation of a line: \(y=mx+b\), Where m = slope
\(y=y\)-intercept, Remember that slope is the rate of change that occurs in a function and that the \(y\)-intercept is the \(y\) value corresponding to \(x=0\).
Since the height of John’s plant is 4 inches tall when he gets it. Time (or \(x\)) is zero. The plant grows 3 inches per year. Therefore, the rate of change of the plant’s height is 3. The \(y\)-intercept represents the starting height of the plant which is 4 inches.
16- The answer is 4
The four-term polynomial expression can be factored completely, by grouping, as follows:
\((x^3-4x^2 )+(+3x-12)=0, x^2 (x-4)+(3)(x-4)=0, (x-4)(x^2+3)=0\)
By the zero product property, set each factor of the polynomial equal to 0 and solve each resulting equation for \(x\). This gives \(x=4\) or \(x=±i\sqrt{3}\), respectively. Because the equation the question asks for the real value of \(x\) that satisfies the equation, the correct answer is 4.
17- The answer is 50
One liter \(= 1000 \space cm^3→ 8 liters = 8000 \space cm^3→8000=16×10×h→h=\frac{8000}{160}=50 \space cm\)
18- The answer is 2
\(x^2-4x+2r=(x- 2)(x- 2p)=x^2+(-2p-2)x+4p\)
On the left side of the equation the coefficient of x is \(-4\) and on the right side of the equation the coefficient of \(x\) is \(-2p-2\). Thus \(-2p-2=-4→p=1\) and \(2r=4p=4(1)=4⇒r=2\)
19- The answer is 176
Let \(L\) be the length of the rectangular and \(W\) be the with of the rectangular. Then,
\(L=2W+6\), The perimeter of the rectangle is 60 meters. Therefore: \(2L+2W=60, L+W=30\)
Replace the value of \(L\) from the first equation into the second equation and solve for \(W\): \((2W+6)+W=30→3W+6=30→3W=24→W=8\)
The width of the rectangle is 8 meters and its length is: \(L=2W+6=2(8)+6=22\)
The area of the rectangle is: length × width = \(22 × 8 = 176\)
20- The answer is 1.03
The initial deposit earns 3 percent interest compounded annually. Thus, at the end of year 1, the new value of the account is the initial deposit of $180 plus 3 percent of the initial deposit: \($180+\frac{3}{100}($180)=$180(1.03)\).
Since the interest is compounded annually, the value at the end of each succeeding year is the sum of the previous year’s value plus 3 percent of the previous year’s value. This is equivalent to multiplying the previous year’s value by 1.03. Thus, after 2 years, the value will be \($180(1.03) (1.03) = $(180)(1.03)^2\); and after 3 years, the value will be \((180)(1.03)^3\); and after \(n\) years, the value will be \((180)(1.03)^n\). Therefore, in the formula for the value for Sara’s account after \(n\) years \((180)(x)^n\), the value of \(x\) is \(1.03\).
Section 2 – Calculator
21- Choice B is correct
In the figure angle A is labeled \((2x-5)\) and it measures 43. Thus, \(2x-5=43\) and \(2x=48\) or \(x=24\).
That means that angle B, which is labeled \((4x)\), must measure \(4×24=96\).
Since the three angles of a triangle must add up to \(180\), \(43+96+y-3=180\), then:
\(y+136=180→y=180-136=44\)
22- Choice B is correct
Since \(f(x)\) is linear function with a positive slop, then when \(x=1\), \(f(x)\) is maximum and when \(x=-3\), \(f(x)\) is minimum. Then the ratio of the minimum value to the maximum value of the function is: \(\frac{f(-3)}{f(1)}=\frac{4(-3)-1}{4(1)-1}=\frac{-13}{3}=-\frac{13}{3}\)
23- Choice C is correct
There can be 0, 1, or 2 solutions to a quadratic equation. In standard form, a quadratic equation is written as: \(ax^2+bx+c=0\)
For the quadratic equation, the expression \(b^2-4ac\) is called the discriminant. If the discriminant is positive, there are 2 distinct solutions for the quadratic equation. If the discriminant is 0, there is one solution for the quadratic equation and if it is negative the equation does not have any solutions.
To find number of solutions for \(4x^2=2x+2\), first, rewrite it as \(4x^2-2x-2=0\).
Find the value of the discriminant. \(b^2-4ac=(-2)^2-4(4)(-2)=4+32=36\)
Since the discriminant is positive, the quadratic equation has two distinct solutions.
24- Choice A is correct
Of the 44 employees, there are 12 females under age 45 and 8 males age 45 or older. Therefore, the probability that the person selected will be either a female under age 45 or a male age 45 or older is: \(\frac{12}{44}+\frac{8}{44}=\frac{20}{44}=\frac{5}{11}\)
25- Choice D is correct
divide each side of the inequality by 2. \(6n-8≥2\) yields the inequality \(3n- 4 ≥ 1\). Now added 6 from each side of the inequality. \(3n+2≥7\) Therefore, the least possible value of \(3n + 2\) is \(7\).
26- Choice D is correct
To solve the equation for y, multiply both sides of the equation by the reciprocal of \(\frac{12}{7}\), which is \(\frac{7}{12}\), this gives \((\frac{12}{7})×\frac{7}{12} y=\frac{3}{5}×(\frac{12}{7})\), which simplifies to \(y=\frac{36}{35}\).
27- Choice A is correct
Subtracting \(3x\) and adding 2 to both sides of \(3x+6≥5x-2\) gives \(8≥ 2x\) and \(4≥x\). Therefore, \(x\) is a solution to \(3x+6≥5x-2\) if and only if \(x\) is less than or equal to 4 and \(x\) is NOT a solution to \(3x+6≥5x-2\) if and only if \(x\) is greater than 4. Of the choices given, only 6 is greater than 4 and, therefore, cannot be a value of \(x\).
28- Choice A is correct
Given the two equations, substitute the numerical value of a into the second equation to solve for \(x\). \(a=\sqrt{5}, 6a=\sqrt{12x}\)
Substituting the numerical value for a into the equation with \(x\) is as follows.
\(6(\sqrt{5})=\sqrt{12x}\), From here, distribute the 4.
\(6\sqrt{5}=\sqrt{12x}\) Now square both side of the equation. \((6\sqrt{5})^2=(\sqrt{12x})^2\) Remember to square both terms within the parentheses. Also, recall that squaring a square root sign cancels them out. \(6^2 \sqrt{5}^2=12x, 36(5)=12x, 180=12x, x=15\)
29- Choice B is correct
First square both sides of the equation to get \(-4m+5=m^2\)
Subtracting both sides by \(-4m+5\) gives us the equation \(m^2+4m-5=0\)
Here you can solve the quadratic equation by factoring to get \((m-1)(m+5)=0\)
For the expression \((m-1)(m+5)\) to equal zero, \(m=1\) or \(m=-5\)
The Absolute Best Book to Ace the SAT Math Test
30- Choice D is correct
Substituting 4 for \(x\) and 10 for \(y\) in \(y=2nx-6\) gives \(10=2(n)(4)-6\),
which gives \(n=2\). Hence, \(y=4x-6\). Therefore, when \(x = 11\), the value of \(y\) is \(y=2(2)(11)-6 =44-6= 38\).
31- Choice C is correct
The best way to deal with changing averages is to use the sum.
Use the old average to figure out the total of the first 5 scores:
Sum of first 5 scores: \((5)(89)=445\)
Use the new average to figure out the total she needs after the 6th score:
Sum of 6 score: \((6)(90)=540\)
To get her sum from \(445\) to \(540\), Mary needs to score \(540-445=95\).
32- Choice C is correct
A zero of a function corresponds to an \(x\)-intercept of the graph of the function in the \(xy\)-plane. Therefore, the graph of the function \(g(x)\), which has two distinct zeros, must have two \(x\)-intercepts. Only the graph in choice C has two \(x\)-intercepts.
33- Choice C is correct
The fastest way to find the answer is to pick numbers. Pick a number for \(x\) that has a remainder of 6 when divided by 9, such as 15. Increase the number you picked by 6. In this case \(15+8=23\). Now divide 23 by 9, which gives you the remainder 5. Therefore, the answer is 5.
34- Choice A is correct
$0.5 per 10 minute to use car. This per-minute rate can be converted to the hourly rate using the conversion 1 hour = 60 minutes, as shown below.
\(\frac{0.5}{10 \space minute}×\frac{60 \space minutes}{1 \space hours}=\frac{$(0.5×6)}{hour}\), Thus, the car costs \($(0.5 × 6)\) per hour.
Therefore, the cost \(c\), in dollars, for \(h\) hours of use is \(c=(0.5×6)h\),
Which is equivalent to \(c=0.5(6h)\)
35- Choice B is correct
Because Jack walks 40 meters in 12 seconds, and 2 minutes is equal to 120 seconds, use the proportion to solve. \(\frac{40 \space meters}{12 \space sec}=\frac{x \space meters}{120 \space sec}\)
The proportion can be simplified to \(\frac{40}{12}=\frac{x}{120}\) then each side of the equation can be multiplied by 120, giving \(\frac{(120)(40)}{12}=x=400\).
Therefore, 400 meters is the distance Jack will walk in 2 minutes.
36- Choice A is correct
It is given that \(g(4)=9\). Therefore, to find the value of \(f(g(4))\), then \(f(g(4))=f(9)=16\)
37- Choice B is correct
\(28\%\) of the books are Mathematics books and \(16\%\) of the books are English books. Thus, number of Mathematics books: \(0.28×800=224\), Number of English books: \(0.16×800=128\)
The product of number of Mathematics and number of English books: \(224×128=28,672\)
38- Choice C is correct
All central angles in a circle sum up to 360 degrees. Thus, the angle \(α\) is: \(0.28×360=100.8^\circ\)
The angle \(β\) is: \(0.16×360=57.6^\circ\)
39- Choice C is correct
According to the graph, \(50\%\) of the books are in the Mathematics and Chemistry sections.
Therefore, there are 400 books in these two sections. \(0.50 × 800 = 400\)
\(γ+α=400\), and \(γ=\frac{2}{3}α\), Replace \(γ\) by \(\frac{2}{3} α\) in the first equation.
\(γ+α=400→\frac{2}{3} α+α=400→\frac{5}{3} α=400\)→multiply both sides by \(\frac{5}{3}\)
\((\frac{3}{5}) \frac{5}{3} α=400×(\frac{3}{5})→α=\frac{400×3}{5}=240\), \(α=240→γ=\frac{2}{3} α→γ=\frac{2}{3}×240=160\)
There are 160 books in the Chemistry section.
40- Choice D is correct
The line passes through the origin, \((5, m)\) and \((m, 15)\).
Any two of these points can be used to find the slope of the line. Since the line passes through \((0, 0)\) and \((5,m)\), the slope of the line is equal to \(\frac{m-0}{5-0}=\frac{m}{5}\). Similarly, since the line passes through \((0, 0)\) and \((m,15)\), the slope of the line is equal to \(\frac{15-0}{m-0}=\frac{15}{m}\). Since each expression gives the slope of the same line, it must be true that \(\frac{m}{5}=\frac{15}{m}\), Using cross multiplication gives ,\( \frac{m}{5}=\frac{15}{m}→m^2=75 →m=±\sqrt{75}=±\sqrt{25×3}=±\sqrt{25}×\sqrt{3}=±5\sqrt{3}\)
41- Choice B is correct
To solve a quadratic equation, put it in the \(ax^2+bx+c=0\) form, factor the left side, and set each factor equal to 0 separately to get the two solutions.
To solve \(2x^2=-4x-2\) , first, rewrite it as \(2x^2+4x+2=0\).
Find the value of the discriminant. \(b^2-4ac=(4)^2-4(2)(2)=16-16=0\)
Since the discriminant is zero, the quadratic equation has one solution.
42- Choice D is correct
The area of the triangle is: \(\frac{1}{2}\) AD \(×\) BC and AD are perpendicular to BC. Triangle ADC is a \(30^\circ -60^\circ- 90^\circ\) right triangle. The relationship among all sides of the right triangle \(30^\circ-60^\circ- 90^\circ\) is provided in the following triangle: In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse. And the opposite side of \(60^\circ\) is opposite of \(30^\circ × \sqrt{3}\)
CD = 6, then AD = 6 × \(\sqrt{3}\)
Area of the triangle ABC is: \(\frac{1}{2}\) AD × BC = \(\frac{1}{2} 6\sqrt{3} × 12 = 36\sqrt{3}\)
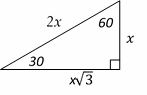
43- Choice B is correct
Here we can substitute 6 for \(x\) in the equation. Thus, \(y-4=3(6+2), y-4=24\)
Adding 4 to both side of the equation: \(y=24+4, y=28\)
44- Choice D is correct
The equation of a circle with center \((h, k)\) and radius \(r\) is \((x-h)^2+(y-k)^2=r^2\). To put the equation \(x^2+y^2+10x+4y=3\) in this form, complete the square as follows:
\(x^2+y^2+10x+4y=3, (x^2+10x)+(y^2+4y)=3\),
\((x^2+10x+25)-25+(y^2+4y+4)-4=3, (x+5)^2+(y+2)^2=32\)
\((x+5)^2+(y+2)^2=(\sqrt{32})^ 2\), Therefore, the radius of the circle is \(\sqrt{32}\).
Best SAT Math Prep Resource for 2022
45- Choice D is correct
By definition, the sine of an acute angle is equal to the cosine of its complement.
Since, angle A and B are complementary angles, therefore: sin A = cos B
46- Choice D is correct
Substituting 10 for \(y\) in \(y=cx^2+d\) gives \(10=cx^2+d\) which can be rewritten as \(10-d=cx^2 \). Since \(y = 10\) is one of the equations in the given system, any solution \(x\) of \(10-d=cx^2\) corresponds to the solution \((x,10)\) of the given system. Since the square of a real number is always nonnegative, and a positive number has two square roots, the equation \(10-d=cx^2\) will have two solutions for \(x\) if and only if (1) \(c > 0\) and \(d <10\) or (2) \(c < 0\) and \(d >10\). Of the values for \(c\) and d given in the choices, only \(c=5\), \(d=5\) satisfy one of these pairs of conditions. Alternatively, if \(c=5\) and \(d=5\), then the second equation would be , \(y=5x^2+5\), The equation above has two real answer.
47- Choice B is correct
\(x\) and \(2z\) are colinear. \(y\) and \(4x\) are colinear. Therefore,
\(x+2z=y+4x\),subtract \(x\) from both sides,then, \(y=2z-3x\)
48- Choice A is correct
It is given that \(g(2)=6\). Therefore, to find the value of \(f(g(6))\), substitute 6 for \(g(2)\).
\(f(g(2))=f(6)=12\).
49- Choice D is correct
Let’s review the options: I. \(|a|<\frac{3}{4}→-\frac{3}{4}<a<\frac{3}{4}\)
Multiply all sides by b. Since, \(b < 0→-b \frac{3}{4}>ab>b \frac{3}{4}\)
II. Since, \(-\frac{3}{4}<a<\frac{3}{4}\), and \(a < 0\)→ \(-\frac{3}{4}a^2>\frac{3}{4} a\) (plug in \(-\frac{1}{2}\), and check!)
III. \(-\frac{3}{4}<a<\frac{3}{4}\), multiply all sides by 4,then: \(-3<4a<3\), add 3 from all sides,then:
\(3-3<4a+3<3+3→0<4a+3<6\), II and III are correct.
50- Choice B is correct
The equation can be rewritten as
\(c-d=2ac\)→(divide both sides by \(c\)) \(1-\frac{d}{c}=2a\), since \(c> 0\) and \(d< 0\), the value of \(-\frac{d}{c}\) is positive. Therefore, 1 plus a positive number is positive. a must be greater than \(\frac{1}{2}\). \(a >\frac{1}{2}\)
51- The answer is 136.5
This is a simple matter of substituting values for variables.
We are given that the 30 cars were washed today, therefore we can substitute that for \(a\).
Giving us the expression \(\frac{15(30)-45}{30}+b\), We are also given that the profit was $150, which we can substitute for \(f(a)\). Which gives us the equation \(150=\frac{15(30)-45}{30}+b\)
Simplifying the fraction gives us the equation \(150=13.5+b\)
And subtracting both sides of the equation by 13.5 gives us \(b=136.5\), which is the answer.
52- The answer is 6.3
The equation of a circle with center \((h, k)\) and radius r is \((x-h)^2+(y-k)^2=r^2\). To put the equation \(x^2+y^2-8x+4y+18=0\) in this form, complete the square as follows:
\(x^2+y^2-8x+4y+18=0, (x^2-8x)+(y^2+4y)+18=0\)
\((x^2-8x+16)-16+(y^2+4y+4)-4+18=0\)
\((x-4)^2+(y+2)^2-20+18=0, (x-4)^2+(y+2)^2-2=0\)
\((x-4)^2+(y+2)^2=2, r^2\) equals 2. Then, \(r=\sqrt{2}\)
The radius of the circle is \(\sqrt{2}\). Thus, the area of the circle is:
\(A=πr^2=3.14(\sqrt{2})^2=3.14×2=6.28\) Round the answer to one decimal place to get 6.3.
53- The answer is 4
Since we are dealing with an absolute value, \(f(a)=10\) means that either \(6-a^2=10\) or
\(6-a^2=-10\), Let’s start with the negative value \((-10)\) and see what we get. If \(6-a^2=-10\), then \(a^2=16\), hence, we get \(a=+4\) or \(-4\), On the other hand, if \(6-a^2=10\), then
\(a=±2i\), Notice that the question states that a is a positive integer, therefore the answer is 4.
54- The answer is 6.
Let \(x\) represent the number of liters of the \(40\%\) solution. The amount of salt in the \(40\%\) solution \((0.40x)\) plus the amount of salt in the \(60\%\) solution \((0.6) × (4)\) must be equal to the amount of salt in the \(48\%\) mixture \((0.48 × (x + 4))\). Write the equation and solve for \(x\).
\(0.40x+0.60(4)=0.48(x+4)→0.40x+2.4=0.48x+1.92→
0.40x-0.48x=1.92-2.4→0.08x=0.48→x=\frac{0.48}{0.08}=6\)
55- The answer is 3.
The function \(f(x)\) is undefined when the denominator of \(\frac{1}{(x-8)^2+25(x-8)+25}\) is equal to zero. The expression \((x-8)^2+10(x-8)+25\) is a perfect square.
\((x-8)^2+10(x-8)+25=((x-8)+5)^2\) which can be rewritten as \((x-3)^2\). The expression \((x-3)^2\) is equal to zero if and only if \(x=3\). Therefore, the value of \(x\) for which \(f(x)\) is undefined is 3.
56- The answer is 336
One of the four numbers is \(x\); let the other three numbers be \(y\), \(z\) and \(w\). Since the sum of four numbers is 560, the equation \(x + y + z+w = 560\) is true. The statement that \(x\) is \(150\%\) more than the sum of the other three numbers can be represented as
\(x = 1.5(y + z+w)\) or \(\frac{x}{1.5}=y+z+w→\frac{2x}{3}=y+z+w\)
Substituting the value \(y+z+w\) in the equation \(x+y+z+w=560\)
gives \(x+\frac{2x}{3}=560→\frac{5x}{3}=560→5x=1,680→x=\frac{1,680}{5}=336\)
57- The answer is 1
Squaring both sides of the equation gives \(12-8a=4a^2\)
Subtracting both sides by \(12-8a\) gives us the equation \(4a^2+8a-12=0\)
Here you can solve the quadratic by factoring to get \((2a+6)(2a-2)=0\)
For the expression \((2a+6)(2a-2)\) to equal zero, \(a=-3\) or \(a=1\)
Since a is a positive integer, \(1\) is the answer.
58- The answer is 52
The area of ∆BED is 30, then: \(\frac{6×AB}{2} =30→6×AB=60→AB=10\)
The area of ∆BDF is 32, then: \(\frac{4×BC}{2}=32→4×BC=64→BC=16\)
The perimeter of the rectangle is = \(2×(10+16)=52\)
College Entrance Tests
The Best Books to Ace the SAT Math Test
Related to This Article
More math articles
- Convert Rational Numbers to a Fraction
- FREE 7th Grade STAAR Math Practice Test
- HSPT Math Formulas
- 10 Most Common 3rd Grade NYSE Math Questions
- 5th Grade NSCAS Math Worksheets: FREE & Printable
- 8th Grade Common Core Math FREE Sample Practice Questions
- How to Use Strip Models to Add Fractions with Like Denominators
- 4th Grade IAR Math Worksheets: FREE & Printable
- What does SAT Stand for?
- How to Add and Subtract Radical Expressions? (+FREE Worksheet!)



















What people say about "Full-Length SAT Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.