Full-Length SAT Math Practice Test

Taking a Full-length SAT Math practice test is the best way to help you get familiar with the test format and feel more confident. Not only will this help you measure your exam readiness and solidify the concepts you’ve learned, but it is the best way to simulate test day.
To help you get the best out of this complete and realistic SAT Math practice test and prepare your mind and body for the actual test, we recommend that you treat this practice test as a real test. Prepare scratch papers, a pencil, a timer, and a calculator and take the test in one sitting and follow the time limits to the minute.
Take the following full-length SAT Math practice test to simulate the test day experience. After you’ve finished, score your tests using the answer keys.
Good luck!

The Absolute Best Book to Ace the SAT Math Test

Time to refine your Math skill with a practice test

Best SAT Math Prep Resource for 2022

SAT Math Practice Test

Section 1
(No Calculator)
20 questions
Total time for this section: 25 Minutes
You may NOT use a calculator on this Section.

1- Which of the following is equivalent to \((-5m^2+4m-2)+(3m^2-3)\)?

A. \(4m+4m^2\)

B. \(-2m^2+4m-5\)

C. \(m^2-4m-5\)

D. \(2m^2+m+5\)

2- If \(3x-y=6, x+2y=2,\) which of the following ordered pairs \((x,y)\) satisfies both equations?

A. \((4, 2)\)

B. \((2, 4)\)

C. \((2,-3)\)

D. \((2,0)\)

3- If \(f(x)=2x+4(2-x)+4\) then \(f(-2x)=\)?

A. \(3x+6\)

B. \(4x-6\)

C. \(2x+4\)

D. \(4x+12\)

4- A line in the \(xy\)-plane passes through origin and has a slope of \((-\frac{3}{5})\). Which of the following points lies on the line?

A. \((2,\frac{3}{5})\)

B. \((4,1)\)

C. \((\frac{3}{4},\frac{4}{5})\)

D. \((\frac{4}{3},-\frac{4}{5})\)

5- If \(18x-7=25\), what is the value of \(10x-12\)?

A. 8

B. 10

C. 14

D. 16

6- Calculate \(f(-3)\) for the following function \(f\).
\(f(x)=2x^2-2x+1\)

A. 5

B. 10

C. 15

D. 25

7- If \(x≠2\) and \(x≠-3\), which of the following is equivalent to \(\frac{1}{\frac{1}{(x-2)}+\frac{1}{(x+3)}}\)?

A.\(\frac{(x-2)(x+3)}{(x-2)-(x+3)}\)

B. \(\frac{(x-2)(x+3)}{(x-2)+(x+3)}\)

C. \(\frac{(x-2)(x+3)}{(x-2)-(x-3)}\)

D. \(\frac{(x+2)(x-3)}{(x+2)+(x-3)}\)

8- \(y<a+x, y> x+ b\)
In the \(xy\)-plane, if \((1, 2)\) is a solution to the system of inequalities above, which of the following relationships between \(a\) and \(b\) must be true?

A. \(a>b\)

B. \(a<b\)

C. \(a=b\)

D. \(a= b+ a\)

9- Which of the following points lies on the line that goes through the points \((1,6)\) and \((-3,2)\)?

A. \((-8, -2)\)

B. \((-5, -2)\)

C. \((-3, -8)\)

D. \((6, -6)\)

10- If \((ax+2)(bx-3)=8x^2-cx-6\) for all values of \(x\) and \(a+b=6\), what are the two possible values for \(c\)?

A. \((8,-2)\)

B. \((2,-2)\)

C. \((2,- 6)\)

D. \((-4,3)\)

11- What is the equation of the graph?

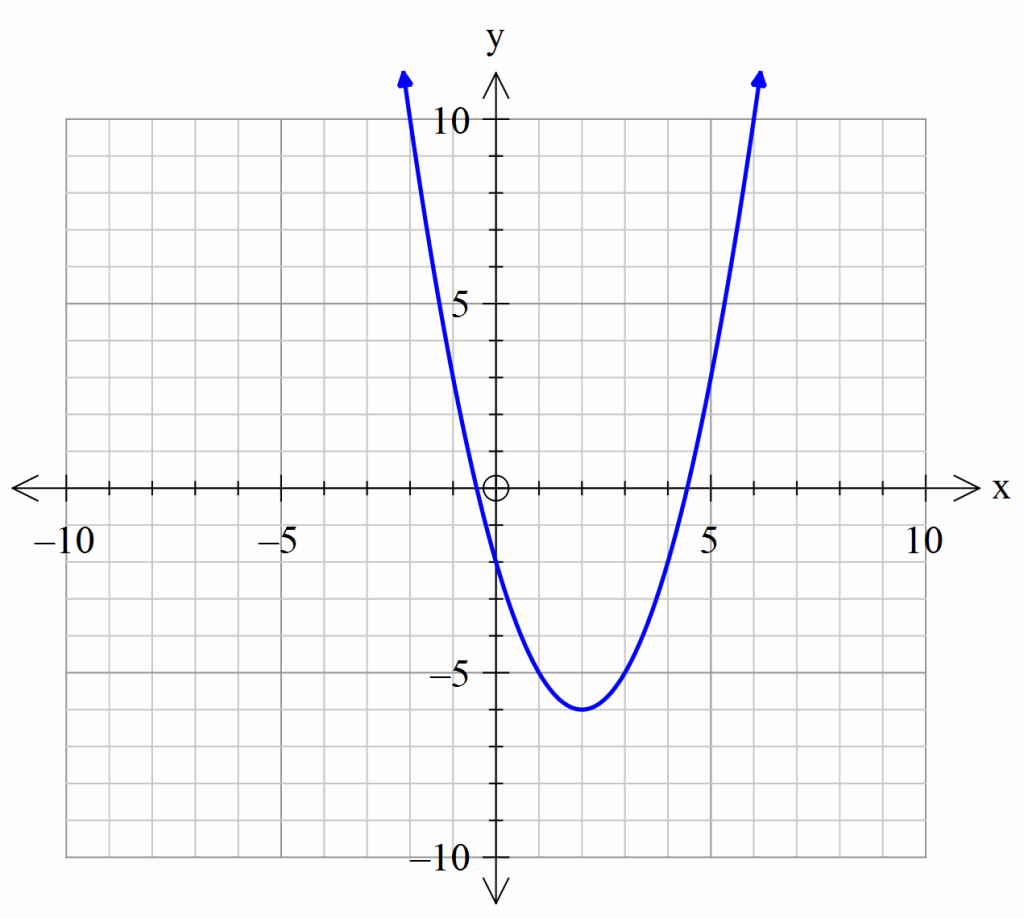
A. \(x^2-4x-2\)

B. \(x^2+2x+4\)

C. \(2x^2-4x-2\)

D. \(2x^2+4x+2\)

12- If \(\frac{8}{3x}=\frac{4}{x-5}\) what is the value of \(\frac{3x}{5}\)?

A. \(-6\)

B. \(-3\)

C. \(-2\)

D. \(6\)

13- Which of the following is an equation of a circle in the \(xy\)-plane with center \((1,-3)\) and a radius with endpoint \((5,2)\)?

A. \((x+1)^2+(y+3)^2=-9\)

B. \((x-1)^2+(y+3)^2=41\)

C. \((x+1)^2+(y-3)^2=-9\)

D. \((x-1)^2+(y-3)^2=41\)

14- Given a right triangle \(∆ABC\) whose \(n∠B=90^\circ\) , \(sin⁡C=\frac{3}{5}\), find \(cos⁡A\)?

A. 1

B. \(\frac{1}{2}\)

C. \(\frac{1}{3}\)

D. \(\frac{3}{5}\)

15- John buys a pepper plant that is 4 inches tall. With regular watering, the plant grows 3 inches a year. Writing John’s plant’s height as a function of time, what does the \(y\)-intercept represent?

A. The \(y\)-intercept represents the rate of growth of the plant which is 3 inches

B. The \(y\)-intercept represents the rate of growth of the plant which is 4 inches per year

C. There is no \(y\)-intercept

D. The \(y\)-intercept represents the starting height of 4 inches

16- For what real value of \(x\) is the equation below true?
\(x^3-4x^2+3x-12=0\)

17- 8 liters of water are poured into an aquarium that’s 16 cm long, 10 cm wide, and 60 cm high. How many centimeters will the water level in the aquarium rise due to this added water? (1 liter of water = 1,000 \(cm^3\))

18- If \(x^2-4x+2r\) factors into \((x-2)(x- 2p)\), and \(r\) and \(p\) are constants, what is the value of \(r\)?

19- The length of a rectangle is 6 meters greater than 2 times its width. The perimeter of the rectangle is 60 meters. What is the area of the rectangle in meters?

20- Sara opened a bank account that earns 3 percent compounded annually. Her initial deposit was $180, and she uses the expression $180\((x)^n\) to find the value of the account after \(n\) years. What is the value of \(x\) in the expression?

21- In the triangle below, if the measure of angle \(A\) is 43 degrees, then what is the value of \(y\)? (the figure is NOT drawn to scale)

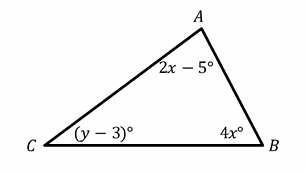
A. 38

B. 44

C. 56

D. 62

22- What is the ratio of the minimum value to the maximum value of the following function?
\(?(?)=4?−1, −3≤?≤1\)

A.\(−\frac{3}{13}\)

B. \(−\frac{13}{3}\)

C. \(−\frac{7}{11}\)

D. \(\frac{11}{7}\)

23- The equation \(4x^2=2x+2\) has how many distinct real solutions?

A. 0

B. 1

C. 2

D. 4

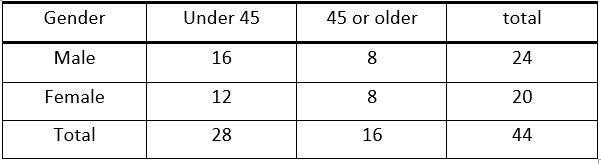
24- The table above shows the distribution of age and gender for 44 employees in a company. If one employee is selected at random, what is the probability that the employee selected to be either a female under age 45 or a male age 45 or older?

A. \(\frac{5}{11}\)

B. \(\frac{35}{44}\)

C. \(\frac{4}{5}\)

D. \(\frac{10}{11}\)

25- If \(6?−8≥2\), what is the least possible value of \(3?+2\)?

A. \(−7\)

B. \(−3\)

C. \(3\)

D. \(7\)

26- If \(\frac{7}{12}y=\frac{3}{5}\), what is the value of \(y\)?

A. \(\frac{5}{6}\)

B. \(\frac{5}{4}\)

C. \(\frac{35}{36}\)

D. \(\frac{36}{35}\)

27- Which of the following numbers is NOT a solution to the inequality \(3x+6≥5x-2\)?

A. \(6\)

B. \(3\)

C. \(-2\)

D. \(-8\)

28- If the following equations are true, what is the value of \(x\)?
\(a=\sqrt{5}\)
\(6a=\sqrt{12x}\)

A. 15

B. 20

C. 25

D. 30

29- If \(\sqrt{-4m+5}=m\), what is (are) the value(s) of \(m\)?

A. \(0\)

B. \(1,-5\)

C. \(1, 5\)

D. \(-1, 5\)

30- If \(y=2nx-6\), where n is a constant, and when \(x=4\), \(y=10\), what is the value of y when \(x=11\)?

A. 10

B. 12

C. 26

D. 38

31- Mary’s average score after 5 tests is 89. What score on the 6th test would bring Mary’s average up to exactly 90?

A. 85

B. 90

C. 95

D. 100

32- If the function \(g(x)\) has two distinct zeros, which of the following could represent the graph of \(g(x)\)?

A.

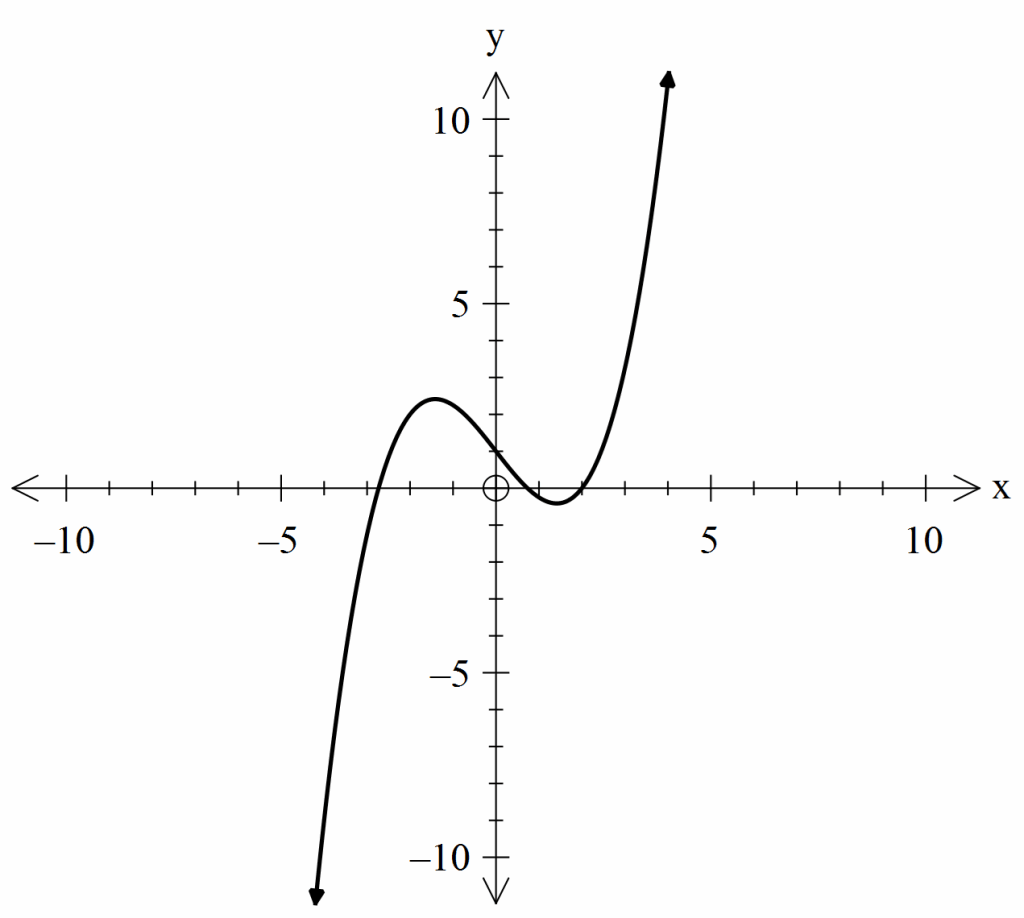
B.

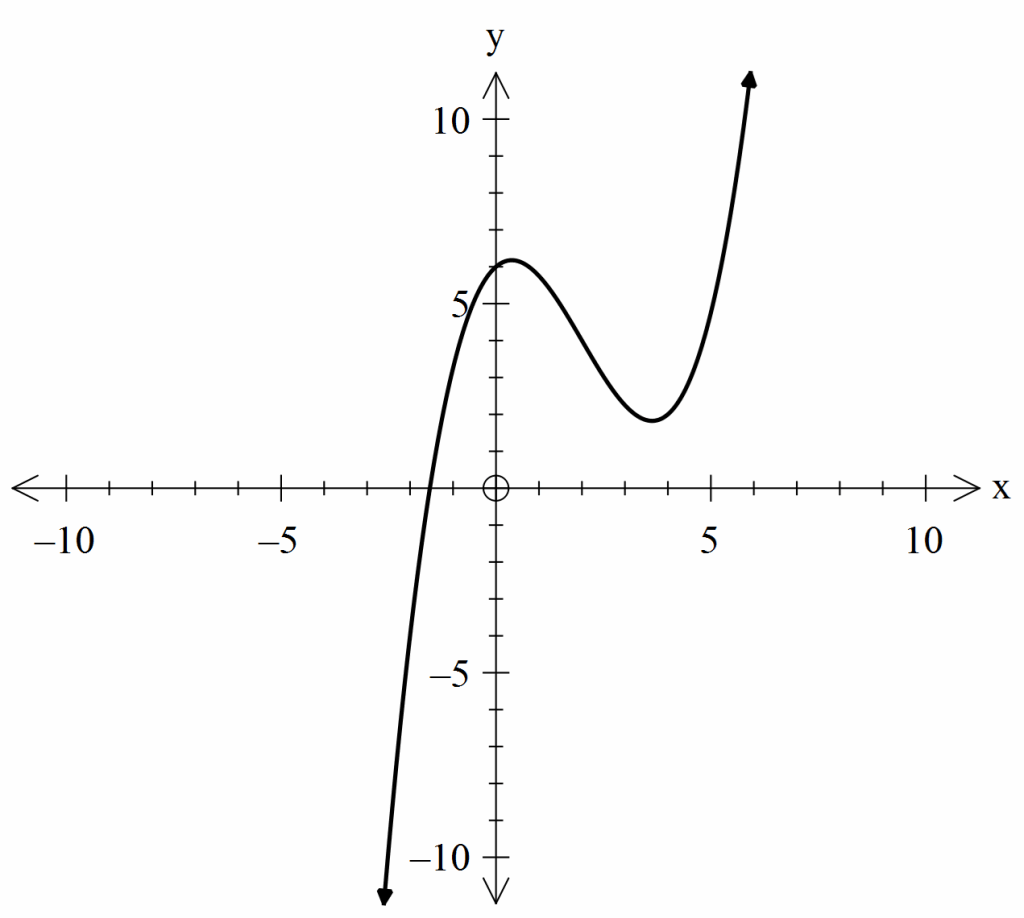
C.

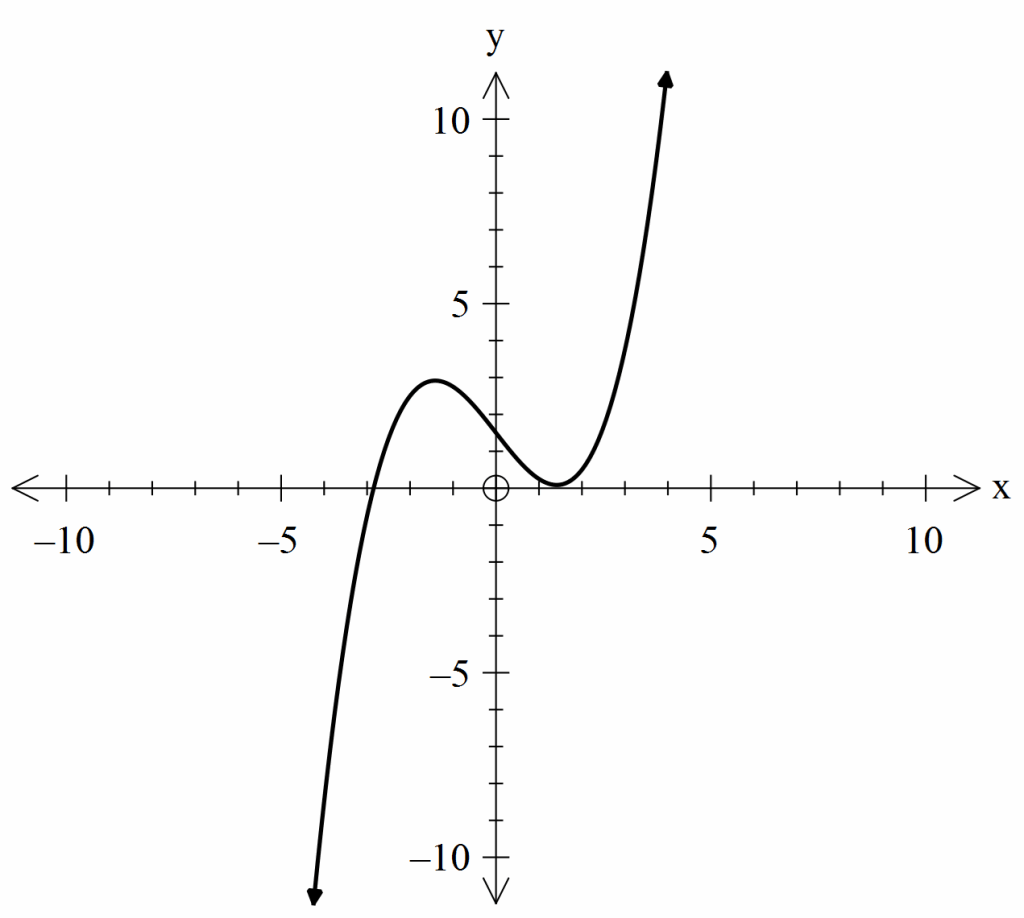
D.

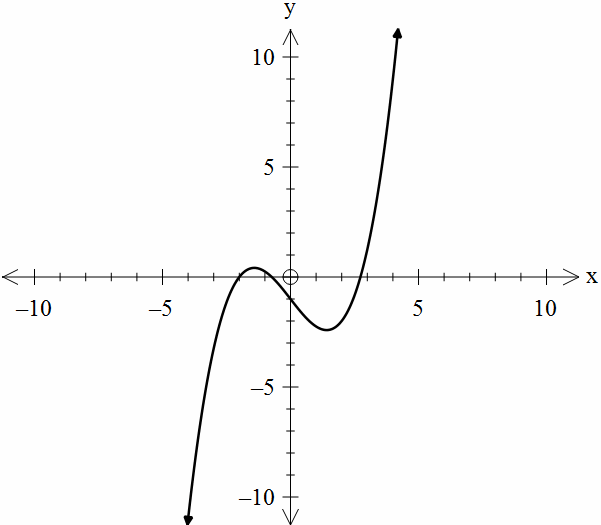
33- If the positive integer \(x\) leaves a remainder of \(6\) when divided by \(9\), what will the remainder be when \(x+8\) is divided by \(9\)?

A. 1

B. 3

C. 5

D. 7

34- The cost of using a car is $0.5 per 10 minutes. Which of the following equations represents the total cost \(c\), in dollars, for h hours of using the car?

A. \(c=0.5(6h)\)

B. \(c=0.5+(6h)\)

C. \(c=\frac{6h}{0.5}\)

D. \(c=0.5-(6h)\)

35- Jack walks 40 meters in 12 seconds. If he walks at this same rate, which of the following is the distance he will walk in 2 minutes?

A. 350 m

B. 400 m

C. 500 m

D. 650 m

36- A function \(g(4)=9\) and \(g(6)=11\). A function \(f(3)=3\) and \(f(9)=16\). What is the value of \(f(g(4))\)?

A. 16

B. 18

C. 20

D. 22

Use the following graph to answer questions 37 to 39.

A library has 800 books that include Mathematics, Physics, Chemistry, English, and History.

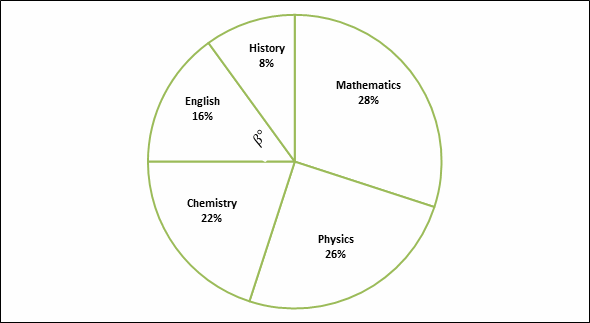
37- What is the product of the number of Mathematics and number of English books in the library?

A. 31,752

B. 28,672

C. 21,168

D. 17,640

38- What are the values of angle \(α\) and \(β\) in the graph?

A. \(90.4^\circ , 54.8^\circ\)

B. \(120.5^\circ, 36.8^\circ\)

C. \(100.8^\circ, 57.6^\circ\)

D. \(108.2^\circ, 54.9^\circ\)

39- The librarians decided to move some of the books in the Mathematics section to the Chemistry section. How many books are in the Chemistry section if now \(γ=\frac{2}{3}α\)?

A. 80

B. 120

C. 160

D. 180

40- In the \(xy\)-plane, the line determined by the points \((5, m)\) and \((m, 15)\) passes through the origin. Which of the following could be the value of \(m\)?

A. \(\sqrt{15}\)

B. \(6\)

C. \(5\sqrt{2}\)

D. \(5\sqrt{3}\)

41- The equation \(2x^2=-4x-2\) has how many distinct real solutions?

A. 0

B. 1

C. 2

D. 3

42- What is the area of the following equilateral triangle if the side BC = 12 cm?

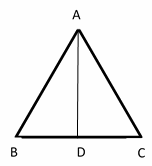
A. \(6\sqrt{3} \space cm^2\)

B. \(8\sqrt{3} \space cm^2\)

C. \(12\sqrt{3} \space cm^2\)

D. \(36\sqrt{3} \space cm^2\)

43- Point A lies on the line with equation \(y-4=3(x+2)\). If the \(x\)-coordinate of A is 6, what is the \(y\)-coordinate of A?

A. 20

B. 28

C. 32

D. 35

44- \(x^2+y^2+10x+4y=3\)
The equation of a circle in the \(xy\)-plane is shown above. What is the radius of the circle?

A. \(\sqrt{24}\)

B. \(\sqrt{18}\)

C. \(\sqrt{24}\)

D. \(\sqrt{32}\)

45- Right triangle ABC is shown below. Which of the following is true for all possible values of angle A and B?

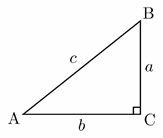
A. \(tan A=tan B\)

B. \(sin A=-cos B\)

C. \(tan^2 A=tan^2 B\)

D. \(cos A=sin B\)

46- \(y=cx^2+d , y=10\)
In the system of equations above, \(c\) and \(d\) are constants. For which of the following values of \(c\) and \(d\) does the system of equations have exactly two real solutions?

A. \(c=3,d=10\)

B. \(c=1,d=-7\)

C. \(c=-3,d=4\)

D. \(c=5,d=5\)

47- From the figure below, which of the following must be true? (figure not drawn to scale)

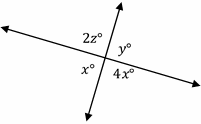
A. \(y = z\)

B. \(y=2z-3x\)

C. \(y≥x\)

D. \(y+4x=2z\)

48- A function \(g(x)\) satisfies \(g(2)=6\) and \(g(5)=7\). A function \(f(x)\) satisfies \(f(6)=12\) and \(f(7)=22\). What is the value of \(f(g(2))\)?

A. 12

B. 22

C. 32

D. 42

49- If \(|a|<\frac{3}{4}\), then which of the following is true? \((b<0)\)?
I. \(-\frac{3b}{4}<ba<\frac{3b}{4}\)
II. \(-\frac{3}{4} a>a^2>\frac{3}{4}a\) if \(a<0\)
III. \(0<4a+3<6\)

A. I only

B. III only

C. I and III only

D. II and III

50- \(\frac{c-d}{c}=2a\)
In the equation above, if \(c\) is positive and \(d\) is negative, which of the following must be true?

A. \(a<\frac{1}{2}\)

B. \(a>\frac{1}{2}\)

C. \(a>1\)

D. \(a<1\)

51- The profit in dollars from a carwash is given by the function \(P(x)=\frac{15a-45}{a}+b\), where \(a\) is the number of cars washed and \(b\) is a constant. If 30 cars were washed today for a total profit of $150, what is the value of \(b\)?

52- In the standard \((x,y)\) coordinate system plane, what is the area of the circle with the following equation? (π=3.14) (Round the answer to one decimal place)
\(x^2+y^2-8x+4y+18=0\)

53- \(f(a)=|6-a^2 |\), where a is a positive integer. If \(f(a)=10\), what is the value of a that satisfies the equation above?

54- How many liters of a \ solution (40\%\) salt must be added to 4 liters of a solution that is \(60\%\) salt to obtain a \(48\%\) salt solution?

55- \(f(x)=\frac{1}{(x-8)^2+10(x-8)+25}\)
For what value of \(x\) is the function \(f(x)\) above undefinded?

56- The sum of four numbers is 560. One of the numbers, \(x\) is \(150\%\) more than the sum of the other three numbers. What is the value of \(x\)?

57- If \(a\) is a positive integer and \(\sqrt{12-8a}=2a\), what is the value of \(a\)?

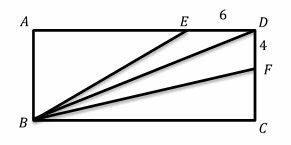
58- In the following figure, ABCD is a rectangle, E and F are points on AD and DC, respectively, and DE = 6 and DF = 4. The area of ∆BED is 30, and the area of ∆BDF is 32. What is the perimeter of the rectangle?

College Entrance Tests

The Best Books to Ace the SAT Math Test

Answers and Explanations