Full-Length PSAT Math Practice Test

Taking the Full-length PSAT Math practice exam is the top method of helping someone get acquainted with the exam’s format and feel more positive. This will not just assist one in figuring out if they are ready to take the exam, it also solidifies your knowledge of the related concepts and is the top method of simulating taking a real exam.
To assist you in getting the most from this comprehensive and realistic PSAT Math practice exam and preparing your body as well as your mind to take a real exam, it’s recommended to act like it’s an actual exam. Prepare some scratch papers, get your pencil, as well as a timer and calculator ready and do the exam all at once and follow the real-time restrictions exactly.
Do the subsequent full-length PSAT Math practice exam to mimic the testing date experience. After you get done, see what your score is by utilizing the proper answer keys.

The Absolute Best Book to Ace the PSAT Math Test

Time to refine your Math skill with a practice test

Best PSAT Math Prep Resource for 2024

PSAT Math Practice Test

Two Sections
Total number of questions: 48
Section 1 (Non-Calculator): 17 questions
Section 2 (Calculator): 31 questions
Total time for two parts: 70 Minutes

PSAT Math Practice Test

Section 1 (Non-Calculator)
17 questions
Total time for two parts: 70 Minutes

1- Which of the following is the solution to the following inequality?
\(12x-14>10x+5-3x+1\)

A. \(x<3\)

B. \(x>3\)

C. \(x≤4\)

D. \(x>4\)

2- If \(f(x^2 )=10-5x\), for all positive value of \(x\), what is the value of \(f(169)\)?

A. \(-55\)

B. \(-20\)

C. \(20\)

D. \(55\)

3- If a and b are solutions of the following equation, which of the following is the ratio \(\frac{a}{b}\)? \((a>b)\)
\(8x^2-5x+8=7x^2+x+15\)

A. \(-\frac{1}{7}\)

B. \(-\frac{1}{5}\)

C. \(-5\)

D. \(-7\)

4- A line in the \(xy\)-plane passes through the origin and has a slope of \(-\frac{2}{3}\). Which of the following points lies on the line?

A. \((2,1)\)

B. \((6, 4)\)

C. \((6,3)\)

D. \((9,3)\)

5- John works for an electric company. He receives a monthly salary of \($3,600\) plus \(4\%\) of all his monthly sales as a bonus. If \(?\) is the number of all John’s sales per month, which of the following represents John’s monthly revenue in dollars?

A. \(0.04x\)

B. \(0.96x-3,800\)

C. \(0.4x+3,800\)

D. \(0.04x+3,600\)

6- What is the value of \(f(-3)\) for the following function \(f\)?
\(f(x)=3x^2+3x+2\)

A. 5

B. 10

C. 15

D. 20

7- If \(x≠-2\) and \(x≠6\), which of the following is equivalent to \(\frac{1}{\frac{1}{x-6}+\frac{1}{x+2}}\)?

A. \(\frac{(x-6)(x+2)}{2x-4}\)

B. \(\frac{2x-4}{(x-6)(x+2)}\)

C. \(\frac{2x+4}{(x-6)(x+2)}\)

D. \(\frac{(x-6)(x+2)}{2x+4}\)

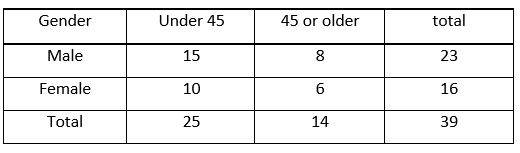
8- The table above shows the distribution of age and gender for 39 employees in a company. If one employee is selected at random, what is the probability that the employee selected to be either a female under age 45 or a male age 45 or older?

A. \(\frac{5}{39}\)

B. \(\frac{6}{39}\)

C. \(\frac{6}{13}\)

D. \(\frac{5}{6}\)

9- If a parabola with equation \(y=ax^2+6x+16\), where a is constant, passes through point \((-2, 8)\), what is the value of \(a^2\)?

A. 1

B. 2

C. 3

D. 4

10- If \(a, b\) and c are positive integers and \(4a=6b=10c\), then the value of \(2a+3b-4c\) is how many times the value of a?

A. 2.4

B. 2.6

C. 3.5

D. 4.2

11- What is the length of AB in the following figure if AE=10, CD=16, and BC=20?

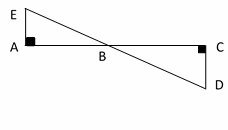
A. 3.8

B. 8.8

C. 12.5

D. 24.6

12- What is the solution of the following system of equations? \(\begin{cases}\frac{x}{3}+\frac{4y}{6}=1 ,y-x=6 \end{cases}\)

A. \(x=5,y=-3\)

B. \(x=-3,y=5\)

C. \(x=-3,y=3\)

D. \(x=3,y=3\)

13- John buys a pepper plant that is 4 inches tall. With regular watering, the plant grows 8 inches a year. Writing John’s plant’s height as a function of time, what does the intercept represent?

A. The y-intercept represents the rate of growth of the plant which is 8 inches

B. The y-intercept represents the starting height of 6 inches

C. The y-intercept represents the rate of growth of a plant which is 4 inches per year

D. There is no y-intercept

14- The length of a rectangle is 8 meters greater than 2 times its width.  The perimeter of the rectangle is 88 meters.  What is the area of the rectangle in meters? __________

15- In the following equation, what is the value of \(y-4x\)? ___________
\(\frac{2y}{9}=x-\frac{1}{9}x+4\)

16- What is the value of \(x\) in the following equation?
\(\frac{x^2-4}{x+2}+4(x+3)=20\)

17- If\(x≠0\), what is the value of \(\frac{(6(x)(y^3 ))^2}{x^2 (3y^2)^3}\)? _____________

PSAT Math Practice Test

Section 2 (Calculator)
31 questions
Total time for two parts: 70 Minutes

18- A football team won exactly 72% of the games it played during the last session. Which of the following could be the total number of games the team played last season?

A. 40

B. 50

C. 55

D. 60

19- If a gas tank can hold 30 gallons, how many gallons does it contain when it is \(\frac{5}{6}\) full?

A. 20

B. 25

C. 62.5

D. 100

20- In the ??-plane, the point \((-2,4)\) and \((6,20)\) are on line A. Which of the following equations of lines is parallel to line A?

A. \(y= \frac{x}{2}\)

B. \(y=x\)

C. \(y=2x\)

D. \(y=3x\)

21- If \(y=nx+4\), where n is a constant, and when \(x=3\), \(y=22\), what is the value of y when \(x=4\)?

A. 10

B. 24

C. 28

D. 32

22- If \(4+4x\) is\(8\) more than \(12\), what is the value of \(8x\)?

A. 32

B.38

C. 62

D. 84

23- If \(x\) is greater than\(-1\) and less than \(1\) and\(x≠0\), which of the following is true?

A. \(x>\sqrt{x^2+1})>\sqrt{x^2}+1\)

B.\(x<\sqrt{x^2}+1<sqrt{x^2+1}\)

C. \(\sqrt{x^2+1})<x<\sqrt{x^2}+1\)

D.\(\sqrt{x^2}+1>sqrt{x^2+1}>x\)

24- The sum of eight different negative integers is \(-100\). If the smallest of these integers is \(-16\), what is the largest possible value of one of the other five integers?

A. \(-14\)

B. \(-9\)

C. \(–5\)

D. \(-1\)

25- The capacity of a red box is \(40\%\) bigger than the capacity of a blue box. If the red box can hold \(35\) equal-sized books, how many of the same books can the blue box hold?

A. 20

B.22

C. 25

D.30

Questions 9 and 11 are based on the following data

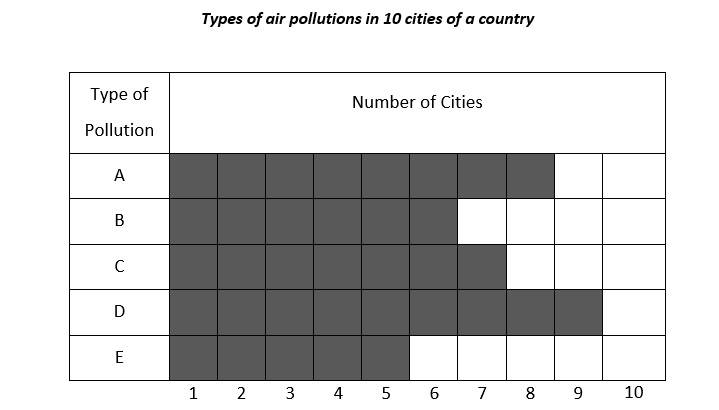
26- If a is the mean (average) of the number of cities in each pollution type category, b is the mode, and c is the median of the number of cities in each pollution type category, then which of the following must be true?

A. \(a<b<c\)

B. \(b<a<c\)

C. \(a=c\)

D. \(b<c=a\)

27- What percent of cities are in the type of pollution A, C, and E respectively?

A. \(60\%, 40\%, 90\%\)

B.\(30\%, 40\%, 90\%\)

C. \(30\%, 40\%, 60\%\)

D. \(80\%, 70\%, 50\%\)

28- How many cities should be added to the type of pollution E until the ratio of cities in the type of pollution E to cities in the type of pollution D will be 0.8?

A. 2.2

B.3.5

C. 4.2

D.5.1

29- What is the ratio of the minimum value to the maximum value of the following function?
\(-4≤x≤5\)
\(f(x)=-2x+2\)

A. \(-1\)

B. \(\frac{-4}{5}\)

C. \(\frac{6}{10}\)

D.\(\frac{8}{7}\)

30- In the following right triangle, if the sides AB and AC become one-third shorter, what will be the ratio of the perimeter of the triangle to its area?

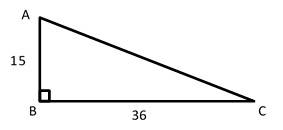
A. \(\frac{1}{2}\)

B. 1

C. 2

D. 3

31- The ratio of boys and girls in a class is 5:9. If there are 84 students in the class, how many more boys should be enrolled to make the ratio 1:1?

A. 12

B.18

C. 24

D.30

Questions 15 to 17 are based on the following data

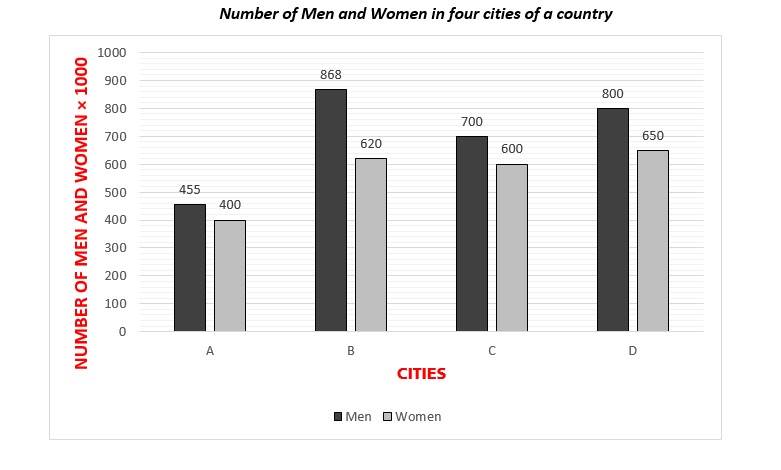
32- What’s the maximum ratio of women to men in the four cities?

A. 0.88

B. 0.91

C. 0.96

D.0.98

33- What’s the ratio of the percentage of men in City A to the percentage of women in City C?

A. 0.9

B. 0.95

C. 1.23

D. 1.38

34- How many women should be added to city D until the ratio of women to men is 1.4?

A. 470

B. 480

C. 495

D. 500

35- If \(f(x)=-2x+2(2x+3)+1\) then \(f(-3x)=\)?

A. \(5x\)

B. \(-6x+4\)

C. \(-6x+7\)

D. \(6x-7\)

36- If a car has 60-liter petrol and after one hour of driving the car uses 7.5-liter petrol, how much petrol will remain after-hours driving?

A. \(60+7.5x\)

B. \(60-7.5x\)

C. \(60×7.5x\)

D. \(60÷7.5x\)

37- In the triangle below, if the measure of angle is 43 degrees, then what is the value of? (the figure is NOT drawn to scale)

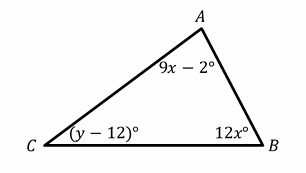
A. 89

B. 90

C. 91

D. 96

38- The following graph shows the marks of six students in mathematics. What is the mean (average) of the marks?

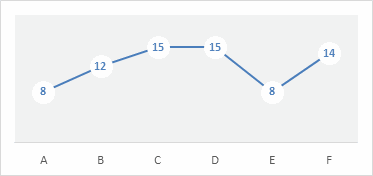
A. 10

B. 12

C. 14

D. 15

39- In the rectangle below if  \(y > 10\) cm and the area of a rectangle is 96 cm\(^2\) and the perimeter of the rectangle is 40 cm, what is the value of and respectively?

A. 6, 12

B. 8, 10

C. 8, 11

D. 8, 12

40- If \(\frac{a-b}{2b}=\frac{5}{9}\), then which of the following must be true?

A. \(\frac{a}{b}=\frac{11}{21}\)

B. \(\frac{a}{b}=\frac{21}{11}\)

C. \(\frac{a}{b}=\frac{21}{10}\)

D. \(\frac{a}{b}=\frac{19}{9}\)

41- Given the right triangle ABC bellow, sec\((β)\) is equal to?

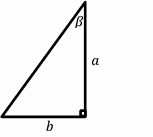
A. \(\frac{a}{b}\)

B. \(\frac{a}{\sqrt{a^2+b^2}}\)

C. \(\frac{\sqrt{a^2+b^2}}{a}\)

D. \(\frac{b}{\sqrt{a^2+b^2}}\)

42- Solve the following inequality.

A. \(|\frac{2x}{3}-4x-6|<4\)

B. \(\frac{6}{-10}>x>-3\)

C. \(\frac{10}{3}<x<10\)

D. \(-10<x<-\frac{10}{3}\)

43- If \(x\) is directly proportional to the square of \(y\), and \(y=3\) when \(x=18\), then when \(x=288 , y= \)?

A. \(\frac{1}{5}\)

B. \(1\)

C. \(5\)

D. \(12\)

44- Which of the following values for \(x\) and \(y\) satisfy the following system of equations?
\(\begin{cases}2x+4y=6 \\x+3y=-20 \end{cases}\)

A. \(x=33,y=-18\)

B. \(x=49,y=-23\)

C. \(x=72,y=-23\)

D. \(x=83,y=-18\)

45- If \(x+4y=\frac{-8y^2+12}{2x}\), what is the value of \((x+2y)^2\)? \((x≠0)\)

46- A ladder leans against a wall forming a \(45^ᵒ\) angle between the ground and the ladder. If the bottom of the ladder is 10 feet away from the wall, how many feet is the ladder?   


      

47- The volume of cube A is \(\frac{1}{4}\) of its surface area. What is the length of the edge of cube A?


        

48- \(f(x)=ax^2+bx+c\) is a quadratic function where a, b and c are constant. The value of \(x\) of the point of intersection of this quadratic function and linear function \(g(x)=x+2\) is \(3\). The vertex of \(f(x)\) is at \((-3, 11)\). What is the product of a, b, and c?

College Entrance Tests

The Best Books to Ace the PSAT Math Test

Answers and Explanations