CLEP College Algebra Math Practice Test Questions
Preparing students for the CLEP College Algebra Math test? Try these free CLEP College Algebra Math Practice questions. Reviewing practice questions is the best way to brush up on your student’s Math skills. Here, we walk you through solving 10 common CLEP College Algebra Math practice problems covering the most important math concepts on the CLEP College Algebra Math test.
These CLEP College Algebra Math practice questions are designed to be similar to those found on the real CLEP College Algebra Math test. They will assess your students’ level of preparation and will give them a better idea of what to study on their exams.
The Absolute Best Book to Ace the CLEP College Algebra Math Test
10 Sample CLEP College Algebra Math Practice Questions
1- If \(A={1,2,4,8,16,24}\) and \(B={1,4,12,24,32,48}\), how many elements are in \(A∪B\)?
A. \(2\)
B. \(3\)
C. \(6\)
D. \(9\)
E. \(12\)
2- The average of five consecutive numbers is \(36\). What is the smallest number?
A. \(38\)
B. \(36\)
C. \(34\)
D. \(12\)
E. \(8\)
3- Which of the following numbers is NOT a solution to the inequality \(2x-5≥3x-1\)?
A. \(-2\)
B. \(-4\)
C. \(-5\)
D. \(-8\)
E. \(-10\)
4- If the following equations are true, what is the value of \(x\)?
\(a=\sqrt{3}\)
\(4a=\sqrt{4x}\)
A. \(2\)
B. \(3\)
C. \(6\)
D. \(12\)
E. \(14)
5- If \(\sqrt{4m-3}=m\), what is (are) the value(s) of m?
A. \(0\)
B. \(1\)
C. \(1, 3\)
D. \(-1, 3\)
E. \( -1,-3\)
6- When a number is subtracted from \(28\) and the difference is divided by that number, the result is \(3\). What is the value of the number?
A. \(2\)
B. \(4\)
C. \(7\)
D. \(12\)
E. \(24\)
7- An angle is equal to the one-ninth of its supplement. What is the measure of that angle?
A. \(9\)
B. \(18\)
C. \(25\)
D. \(60\)
E. \(90\)
8- If \(\sqrt{4m-3}=m\), what is (are) the value(s) of m?
A. \(0\)
B. \(1\)
C. \(1,3\)
D. \(-1,3\)
E. \(-1,-3\)
9-If tan \(\theta=\frac{5}{12}\) and sin \(\theta> 0\), then cos \(\theta= \)?
A. \(-\frac{5}{13}\)
B. \(\frac{12}{13}\)
C. \(\frac{13}{12}\)
D. \(-\frac{12}{13}\)
E. \(0\)
10- Which of the following has the same period and two times the amplitude of graph
\(y = cos \ x\)?
A. \(y=cos \ 2x\)
B. \(y=cos \ (x+2)\)
C. \( y=4 cos \ 2x\)
D. \(y=2+2 cos \ x\)
E. \( y=4+cos \ x\)
Best CLEP College Algebra Math Prep Resource for 2024
Answers:
1- D
The union of A and B is: \(A∪B\)\(={1,2,4,8,12,16,24,32,48}\). There are \(9\) elements in \(A∪B\).
2- C
Let \(x\) be the smallest number. Then, these are the numbers: \(x, x+1, x+2, x+3, x+4\)
average\(=\frac{sum \ of \ terms}{number \ of \ terms}⇒36=\frac{x+(x+1)+(x+2)+(x+3)+(x+4)}{5}⇒36=\frac{5x+10}{5} ⇒
180=5x+10 ⇒170= 5x⇒x=34\)
3- A
Subtracting \(2x\) and adding \(5\) to both sides of \(2x – 5 ≥ 3x – 1\) gives \(-4 ≥ x\). Therefore, \(x\) is a solution to \(2x – 5 ≥ 3x – 1\) if and only if \(x\) is less than or equal to -4 and \(x\) is NOT a solution to\( 2x – 5 ≥ 3x – 1\) if and only if \(x\) is greater than \(-4\). Of the choices given, only \(-2\) is greater than \(-4\) and, therefore, cannot be a value of \(x\).
4- D
Given the two equations, substitute the numerical value of a into the second equation to solve for \(x\). \(a=\sqrt{3}, 4a=\sqrt{4x}\)
Substituting the numerical value for a into the equation with \(x\) is as follows.
\(4(\sqrt{3})=\sqrt{4x}\),From here, distribute the \(4\). \(4\sqrt{3}=\sqrt{4x}\)
Now square both sides of the equation. \((4\sqrt{3})^2=(\sqrt{4x})^2\)
Remember to square both terms within the parentheses. Also, recall that squaring a square root sign cancels them out. \(4^2 \sqrt{3}^2=4x, 16(3)=4x, 48=4x, x=12\)
5- C
First square both sides of the equation to get \(4m-3=m^2\)
Subtracting both sides by \(4m-3\) gives us the equation \(m^2-4m+3=0\)
Here you can solve the quadratic equation by factoring to get \((m-1)(m-3)=0\)
For the phrase \((m-1)(m-3)\) to equal zero, \(m=1 or m=3\)
6- C
Let \(x\) be the number. Write the equation and solve for \(x. (28-x)÷x= 3\)
Multiply both sides by \(x\). \((28-x)= 3x\), then add \(x\) both sides. \(28=4x\), now divide both sides by \(4\).\( x=7\)
7- B
The sum of supplement angles is \(180\). Let \(x\) be that angle. Therefore, \(x+9x\)\(=180\)
\(10 x=180\), divide both sides by \(10\): \(x\)\(=18\)
8- C
First square both sides of the equation to get \(4m-3=m^2\)
Subtracting both sides by \(4m-3\) gives us the equation \(m^2-4m+3=0\)
Here you can solve the quadratic equation by factoring to get \((m-1)(m-3)=0\)
For the phrase \((m-1)(m-3)\) to equal zero, \(m=1 or m=3\)
9- B
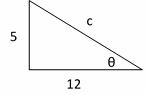
tan\(θ=\frac{opposite}{adjacent}\)
tan\(θ=\frac{5}{12}⇒\) we have the following right triangle. Then
\(c=\sqrt{5^2+12^2 }=\sqrt{25+144}=\sqrt{169}=13\)
\(cosθ=\frac{adjacent}{hypotenuse}=\frac{12}{13}\)
10- D
The amplitude in the graph of the equation \(y=acosbx\) is a. (a and b are constant)
In the equation \(y=cosx\), the amplitude is \(2\) and the period of the graph is \(2π\).
The only choice that has two times the amplitude of graph \(y= cos x\) is \(y=2+2 cos x\)
They both have an amplitude of \(2\) and a period of \(2π\).
Looking for the best resource to help you succeed on the ASTB Math test?
The Best Books to Ace the CLEP College Algebra Math Test
Related to This Article
More math articles
- Quotient Quickies: How to Navigate Decimal Division with Estimations
- 7th Grade PARCC Math FREE Sample Practice Questions
- How to Solve Irrational Functions?
- The Rules of Integral: Complex Subject Made Easy
- What to Consider When Retaking the ACT or SAT
- What is the Best Calculator for the PSAT Test?
- How to Get Better at Math: 7 Comprehensive Tips for Parents with Kids Struggling
- ASVAB Math Formulas
- The Ultimate 6th Grade MCAS Math Course (+FREE Worksheets)
- How Is Math Use in Solar Energy?
What people say about "CLEP College Algebra Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.