Geometry Puzzle – Challenge 67
Time for another mind-blowing math problem to tease your brain and improve your logic skills! For education statistics and research, visit the National Center for Education Statistics.
[include_netrun_products_block from-products="product/ssat-middle-level-math-for-beginners/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Challenge:
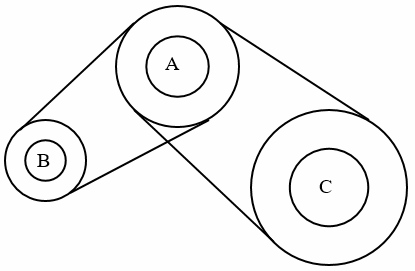
In the figure above, there are three connected wheels. The ratio of the radius of wheel B to the radius of wheel A is 1:3 and the ratio of the radius of wheel A to radius of wheel C is 2:3. When wheel B makes 18 revolutions, how many revolutions does wheel C make? For education statistics and research, visit the National Center for Education Statistics.
A- 2
B- 4
C- 8
D- 54
E- 64
The Absolute Best Book to challenge your Smart Student!
The correct answer is B.
Since, the three wheels are connected; we need to find the ratio of the circumference of all wheels:
The circumference of a circle = 2πr
The ratio of the radius of wheel B to wheel A is 1 to 3. Let \(r_{A }\) be the radius of the wheel A and \(r_{B}\) be the radius of the wheel B. Then:
\(r_{A }= 3r_{B}\)
Circumference of the wheel \(A = 2π r_{A }\)
Replace \(r_{A }\) with \(r_{B }\). Then:
Circumference of the wheel \(A = 2π r_{A } = 2π (3r_{B })= 6π r_{B }\)
The ratio of the circumference of wheel B to A is:
\(2π r_{B} : 2πr_{A } → 2π r_{B } : 6π r_{B} → 2 : 6 → 1 : 3\)
Therefore, the ratio of the circumference of wheel B to A is 1 to 3. (Similar to their radius)
With the same method, the ratio of the circumference of the wheel A to C is 2 to 3.
Therefore, the ratio of the wheels B, A and C is:
B : A =1 : 3 = 2 : 6
A : C = 2: 3 = 6: 9 → B : A : C = 2 : 6 : 9
The ratio of the circumference of the wheel B to the wheel C is 2 to 9 or:
The circumference of the wheel B \(= \frac{2}{9}\) the circumference of the wheel C.
B = 18 → C \(= 18 (\frac{2}{9}) = 4\)
When wheel B makes 18 revolutions, wheel C makes 4 revolutions.The Best Books to Ace Algebra
Original price was: $27.99.$17.99Current price is: $17.99.
Related to This Article
More math articles
- Top 10 Accuplacer Math Prep Books (Our 2023 Favorite Picks)
- PSAT Math Formulas
- Special Right Triangles
- 8th Grade NSCAS Math Worksheets: FREE & Printable
- FREE 5th Grade NYSE Math Practice Test
- FREE SSAT Lower Level Math Practice Test
- 10 Most Common HiSET Math Questions
- 3rd Grade ACT Aspire Math FREE Sample Practice Questions
- 4th Grade KAP Math Worksheets: FREE & Printable
- FREE 3rd Grade Georgia Milestones Assessment System Math Practice Test
What people say about "Geometry Puzzle – Challenge 67 - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.