Full-Length PSAT 10 Math Practice Test-Answers and Explanations
Did you take the PSAT 10 Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
PSAT 10 Math Practice Test Answers and Explanations
PSAT 10 Math Practice Tests Explanations
PSAT 10 Math Practice Test 1:
Section 1 – No Calculator
1- Choice D is correct
\(12x-14>10x+5-3x+1\)→Combine like terms: \(12x-14>7x+6\)→ Subtract \(7x\) from both sides: \(5x-14>6\), Add 14 both sides of the inequality. \(5x>20\), Divide both sides by \(5\).
\(\frac{20}{5}<x→<x>4\)
2- Choice A is correct
\(x^2=169→x=13\) (positive value) Or \(x=-13\) (negative value)
Since x is positive, then: \(f(169)=f(13^2 )=10-5(13)=10-65=-55\)
3- Choice D is correct
\(8x^2-5x+8=7x^2+x+15⇒x^2-6x-7=0\), Find the factors of the quadratic equation.
\(→(x-7)(x+1)=0→x=7 or x=-1, a>b\), then: \(a=7\) and \(b=-1\), \(\frac{a}{b}=\frac{7}{-1}=-7\)
4- Choice D is correct
First, find the equation of the line. All lines through the origin are of the form \(y=mx\), so the equation is \(y=-\frac{2}{3}x\). Of the given choices, only choice \(C (6,-4)\), satisfies this equation:
\(y=-\frac{2}{3}x→-4=-\frac{2}{3}(6)=-4\)
5- Choice D is correct
\(?\) is the number of all John’s sales per month and \(4\%\) of it is: \(4\%×x=0.04x\)
John’s monthly revenue: \(0.04x+3,600\)
6- Choice D is correct
The input value is \(-3\). Then: \(x=-3\), \(f(x)=3x^2+3x+2=3(-3)^2+3(-3)+2=20\)
7- Choice A is correct
To rewrite \(\frac{1}{\frac{1}{x-6}+\frac{1}{x+2}}\), first simplify \(\frac{1}{x-6}+\frac{1}{x+2}\)
\(\frac{1}{x-6}+\frac{1}{x+2}=\frac{1(x+2)+1(x-6)}{(x-6)(x+2)}=\frac{2x-4}{(x-6)(x+2)}\)
Then:\(\frac{1}{\frac{1}{x-6}+\frac{1}{x+2}}=\frac{1}{\frac{2x-4}{(x-6)(x+2)}}=\frac{(x-6)(x+2)}{2x-4}\) (Remember, \(\frac{1}{\frac{1}{x}}=x\))
This result is equivalent to the expression in choice A.
8- Choice C is correct
Of the \(39\) employees, there are \(10\) females under age \(45\) and \(8\) males age \(45\) or older. Therefore, the probability that the person selected will be either a female under age \(45\) or a male age \(45\) or older is: \(\frac{10}{39}+\frac{8}{39}=\frac{18}{39}=\frac{6}{13}\)
9- Choice A is correct
Plug in the values of x and y of the point (-2, 8) in the equation of the parabola. Then:
\(8=a(-2)^2+6(-2)+16→8=4a-12+16→8=4a+4\)
\(→4a=8-4=4→a=4/4=1→a^2=(1)^2=1\)
10- Choice A is correct
\(4a=6b→b=\frac{2a}{3} and 4a=10c→c=\frac{2a}{5}\)
\(2a+3b-4c=2a+3(\frac{2a}{3})-4(\frac{2a}{5})=2a+2a-\frac{8a}{5}=\frac{(20-8)a}{5}=\frac{12a}{5}=2.4a\)
The Absolute Best Book to Ace the PSAT 10 Math Test
11- Choice C is correct
Two triangles ∆BAE and ∆BCD are similar. Then: \(\frac{AE}{CD}=\frac{AB}{BC}→\frac{10}{16}=\frac{x}{20}→200=16x→x=12.5\)
12- Choice C is correct
\(\begin{cases}\frac{x}{3}+\frac{4y}{6}=1 \\y-x=6 \end{cases}\)→ Multiply the top equation by 3. Then, \(\begin{cases}x+2y=3 \\y-x=6 \end{cases}\)
→Add two equations.
\((3y=9→y=3)\) , plug in the value of (y) into the first equation →\((x=-3)\)
13- Choice C is correct
To solve this problem, first recall the equation of a line:
Where, and Remember that slope is the rate of change that occurs in a function and that the intercept is the value corresponding to .
Since the height of John’s plant is 4 inches tall when he gets it. Time (or ) is zero. The plant grows 8 inches per year. Therefore, the rate of change of the plant’s height is 4. The intercept represents the starting height of the plant which is 4 inches.
14- The answer is 384
Let L be the length of the rectangular and W be the with of the rectangular. Then, \(L=2W+8\)
The perimeter of the rectangle is 88 meters. Therefore: \(2L+2W=88, L+W=44\)
Replace the value of L from the first equation into the second equation and solve for W:
\((2W+8)+W=44→3W+8=44→3W=36→W=12\)
The width of the rectangle is 12 meters and its length is: \(L=2W+8=2(12)+8=32\)
The area of the rectangle is: length × width \(= 12 × 32 = 384\)
15- The answer is 18
\(\frac{2y}{9}=x-\frac{1}{9} x+4\), Multiply both sides of the equation by \(9\). Then: \(9×\frac{2y}{9}=9×(x-\frac{1}{9} x+4)→2y=9x-x+36→2y=8x+36→y=4x+18 →y-4x=18\)
Now, subtract 4x from both sides of the equation. Then: \(y-4x=18\)
16- The answer is 2
First, factorize the numerator and simplify.\(\frac{x^2-4}{x+2} +4(x+3)=20
\frac{(x-2)(x+2)}{(x+2)}+4(x+3)=20\)
Divide both sides of the fraction by \((x+2)\). Then: \(x-2+4x+12=20→5x+10=20\)
Subtract 10 from both sides of the equation. Then: →\(5x=20-10=10→x=\frac{10}{5}=2\)
17- The answer is \(\frac{4}{3}\)
First, simplify the numerator and the denominator. \(\frac{(6(x)(y^3 ))^2}{x^2 (3y^2)^3}\)
Remove \(x^2 y^6\) from both numerator and denominator.\(\frac{36x^2 y^6}{27x^2 y^6}=\frac{36}{27}=\frac{4}{3}\)
Best PSAT 10 Math Prep Resource for 2022
PSAT 10 Math Practice Tests Explanations
PSAT 10 Math Practice Test 2:
Section 2 – No Calculator
18- Choice B is correct
Choices A, C, and D are incorrect because \(72\%\) of each of the numbers is a non-whole number.
A. 40 \(72\% of 40 = 0.72×40=28.8\)
B. 50 \(72\% of 50=0.72×50=36\)
C. 55 \(72\% of 55=0.72×55=39.6\)
D. 60 \(72\% of 60=0.72×60=43.2\)
Only choice B gives a whole number.
19- Choice B is correct
\(\frac{5}{6}×30=\frac{150}{6}=25\)
20- Choice C is correct
The slop of line A is: \(m=\frac{y_2-y_1}{x_2-x_1}=\frac{20-4}{6-(-2)}=2\)
Parallel lines have the same slope and only choice \(C (y=x)\) has slope of 2.
21- Choice C is correct
Substituting 3 for x and 22 for y in \(y = nx+4\) gives \(22=(n)(3)+4\),
which gives \(n=6\). Hence, \(y=6x+4\). Therefore, when \(x = 4\), the value of y is: \(y=(6)(4)+4 = 28\)
22- Choice A is correct
The description \(4+4x\) is \(8\) more than \(12\) can be written as the equation \(4+4x=8+12\), which is equivalent to \(4+4x=20\). Subtracting \(4\) from each side of \(4+4x=20\) gives
\(4x=16\). Since \(8x\) is \(2\) times \(4x\), multiplying both sides of \(4x=16\) by \(2\) gives \(8x=32\)
23- Choice D is correct
Let \(x\) be equal to \(0.5,-0.5\), then: \(x=-0.5,0.5\)
\(\sqrt{x^2+1}=\sqrt{(0.5)^2+1}=\sqrt{1.25}≈1.12 . \sqrt{x^2} +1=\sqrt{(0.5)^2}+1=0.5+1=1.5\)
\(\sqrt{x^2+1}=\sqrt{(-0.5)^2+1}=\sqrt{1.25}≈1.12. \sqrt{x^2} +1=\sqrt{-0.5)^2}+1=0.5+1=1.5\)
Then, option D is correct. D. \(\sqrt{x^2 }+1>\sqrt{x^2+1}>x\)
24- Choice B is correct
The smallest number is \(-16\). To find the largest possible value of one of the other five integers, we need to choose the smallest possible integers for four of them. Let \(x\) be the largest number. Then: \(-100=(-16)+(-15)+(-14)+(-13)+(-12)+(-11)+(-10)+x→ -100=-91+x, →x=-100+91=-9\)
25- Choice C is correct
The capacity of a red box is \(40\%\) bigger than the capacity of a blue box and it can hold \(35\) books. Therefore, we want to find a number that \(40\%\) is bigger than that number is \(35\). Let \(x\) be that number. Then: \(1.4×x=35\), Divide both sides of the equation by \(1.4\). Then: \(x=\frac{35}{1.40}=25\)
26- Choice C is correct
Let’s find the mean (average), mode, and median of the number of cities for each type of pollution. Number of cities for each type of pollution: \(8, 6, 7, 9, 5\)
??????? (????) \(=\frac{sum \ of \ terms}{number \space of \space terms}=\frac{8+6+7+9+5}{5}=\frac{35}{5}=7\)
Median is the number in the middle. To find the median, first list numbers in order from smallest to largest. \(5, 6, 7, 8, 9,\) Median of the data is 7. Mode is the number that appears most often in a set of numbers. Therefore, there is no mode in the set of numbers. Median = Mean, then, c=a
27- Choice D is correct
Percent of cities in the type of pollution A: \(\frac{8}{10}×100=80\%\)
Percent of cities in the type of pollution C: \(\frac{7}{10}×100=70\%\)
Percent of cities in the type of pollution E: \(\frac{5}{10}×100=50\%\)
28- Choice D is correct
Let x be the number of cities that need to be added to the type of pollutions E. Then:
\(\frac{x+5}{9}=0.8→x+5=9×0.8→x+5=7.2→x=2.2\)
29- Choice B is correct
Since \(f(x)\) is linear function with a negative slop, then when \(x=-4,f(x)\) is maximum and when \(x=5,f(x)\) is minimum. Then the ratio of the minimum value to the maximum value of the function is: \(\frac{f(5)}{f(-4)}=\frac{-2(5)+2}{-2(-4)+2}=\frac{-8}{10}=\frac{-4}{5}\)
30- Choice B is correct
AB=15 And BC=36, AC=\(\sqrt{15^2+36^2} =\sqrt{225+1296}=\sqrt{1521}=39\)
Perimeter =\(15+36+39=90\) , Area =\(\frac{36×15}{2}=270\)
In this case, the ratio of the perimeter of the triangle to its area is: \(\frac{90}{270}=\frac{1}{3}\)
If the sides AB and AC become one third shorter, then: AB=5 And AC=13
BC=\(\sqrt{13^2-5^2}=\sqrt{169-25}=\sqrt{144}=12\), Perimeter =\(5+12+13=30\)
Area =\9\frac{12×5}{2}=30\), In this case the ratio of the perimeter of the triangle to its area is: \(\frac{30}{30}=1\)
31- Choice B is correct
The ratio of boys to girls is 5:9. Therefore, there are 5 boys out of 14 students. To find the answer, first, divide the total number of students by 14, then multiply the result by 5.
\(84 ÷ 14 = 6 ⇒ 5 × 6 = 30\), There are 30 boys and \(54 (84 – 30)\) girls. So, 24 more boys should be enrolled to make the ratio 1:1
32- Choice A is correct
Ratio of women to men in city A: \(\frac{400}{455}=0.88\)
Ratio of women to men in city B: \(\frac{620}{868}=0.71\)
Ratio of women to men in city C: \(\frac{600}{700}=0.86\)
Ratio of women to men in city D: \(\frac{650}{800}=0.81\)
Choice A provides the maximum ratio of women to men in the four cities.
33- Choice A is correct
Percentage of men in city A = \(\frac{455}{855}×100=56.87\%\)
Percentage of women in city C = \(\frac{600}{1300}×100=46.15\%\)
Percentage of men in city A to percentage of women in city C = \\(frac{56.87}{46.15}=1.23\)
34- Choice A is correct
Let the number of women should be added to city D be \(x\), then:
\(\frac{650+x}{800}=1.4→650+x=800×1.4=1120→x=470\)
35- Choice C is correct
If \(f(x)=-2x+2(2x+3)+1\) , then find \(f(-3x)\) by substituting \(4x\) for every \(x\) in the function. This gives: \(f(-3x)=-2(-3x)+2(2(-3x)+3)+1=6x-12x+6+1\) ,
It simplifies to: \(f(-3x)=6x-12x+6+1=-6x+7\)
36- Choice C is correct
The amount of petrol consumed after \(x\) hours is: \(7.5×x=7.5x\)
Petrol remaining after x hours driving: \(60-7.5x\)
37- Choice A is correct
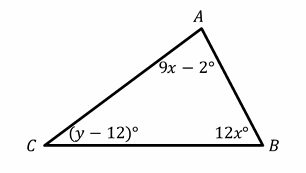
In the figure angle A is labeled \((9x-2)\) and it measures 43. Thus, \(9x-2=43\) and \(9x=45\) or \(x=5\). That means that angle B, which is labeled \((12x)\), must measure \(12×5=60\).
Since the three angles of a triangle must add up to 180, \(43+60+y-12=180\), then: \(y+91=180→y=180-91=89\)
38- Choice A is correct
??????? (????) \(= \frac{sum \space of \space terms}{number \space of \space terms}=\frac{8+12+15+15+8+14}{6}=12\)
39- Choice D is correct
The perimeter of the rectangle is: \(2x+2y=40→x+y=20→x=20-y\)
The area of the rectangle is: \(x×y=96→(20-y)(y)=96→y^2-20y+96=0\)
Solve the quadratic equation by factoring method.
\((y-8)(y-12)=0→y=8\) (Unacceptable, because y must be greater than 10) or \(y=12\)
If \(y=12 →x×y=96→x×12=96→x=8\)
40- Choice D is correct
The equation \(\frac{a-b}{2b}=\frac{5}{9}\) can be rewritten as \(\frac{a}{2b}-\frac{b}{2b}=\frac{5}{9}\), from which it follows that \(\frac{a}{2b}-\frac{1}{2}=\frac{5}{9}\), or \(\frac{a}{2b}=\frac{5}{9}+\frac{1}{2}=\frac{19}{18}.\)⇒\(\frac{a}{b}=\frac{19}{9}\), Subtract 12 from both sides of the equation. Then: \(x+12=10→x=-2\)
41- Choice D is correct
\(Cosβ=\frac{Adjacent \space side}{hypotenuse}\), To find the hypotenuse, we need to use Pythagorean theorem.
\(a^2+b^2=c^2→c=\sqrt{a^2+b^2}, cos (β)=\frac{a}{c}=\frac{a}{\sqrt{a^2+b^2}}, sec(β)=\frac{1}{cos (β)} =\frac{\sqrt{a^2+b^2 }}{a}\)
42- Choice B is correct
\(|\frac{2x}{3}-4x-6|<4.⇒-4<\frac{2x}{3}-4x-6<4\).Multiply both side by 3. ⇒ \(-12<2x-12x-18<12\), add 18 from all sides of the inequality. \(18-12<-10x-18+18<12+18⇒6<-10x<30\), Divide all sides by \(-10\). \(\frac{6}{-10}>x>-3\)
(Remember that when you divide all sides of an inequality by a negative number, the inequality sing will be swapped. < becomes >)
43- Choice D is correct
\(x\) is directly proportional to the square of \(y\). Then: \(x=cy^2
18=c(3)^2→18=9c→c=18/9=2\), The relationship between \(x\) and \(y\) is: \(x=2y^2
x=288, 288=2y^2→y^2=288/2=144→y=12\)
44- Choice B is correct
\(\begin{cases}2x+4y=6 \\x+3y=-20 \end{cases}\)
Multiply the second equation by \(-2\) then,
\(\begin{cases}2x+4y=6 \\-2x-6y=40 \end{cases}\)
Add two equations , \(-2y=46→y=-23\) , plug in the value of y into the second equation, \(x+3y=-20→x+4(-23)=-20→x=49\)
Subtract 12 from both sides of the equation. Then: \(x+12=10→x=-2\)
45- The answer is 6
\(x+4y=\frac{-8y^2+12}{2x}\), Multiply both sides by \(2x\).
\(2x×(x+4y)=2x×((\frac{-8y^2+12}{2x})→2x^2+8xy=-8y^2+12
→2x^2+8xy+8y^2=12→2×(x^2+4xy+4y^2 )=12→x^2+4xy+4y^2=6
x^2+4xy+4y^2=(x+2y)^2, Then: →(x+2y)^2=6\)
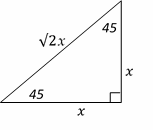
46- The answer is 14.14
The relationship among all sides of special right triangle
\(45^\circ-45^\circ- 90^\circ\) is provided in this triangle: According to picture length of ladder is \(\sqrt{2} x⇒L=10\sqrt{2}=14.14\)
47- The answer is \(\frac{3}{2}\)
Let x be the length of an edge of cube, then the volume of a cube is: \(V=x^3\)
The surface area of cube is: \(SA=6x^2\), The volume of cube A is \(\frac{1}{4}\) of its surface area. Then:
\(x^3=\frac{6x^2)}{4}→x^3=\frac{3}{2}x^2\), divide both side of the equation by \(x^2\). Then: \(\frac{x^3}{x^2} =\frac{3x^2}{2x^2} →x=\frac{3}{2}\)
48- The answer is \(\frac{19}{12}\)
The intersection of two functions is the point with 3 for \(x\). Then:
\(f(3)=g(3) and g(3)=(3+2)=5\),
Then, \(f(2)=5→a(3)^2+b(3)+c=5.⇒9a+3b+c=5\) (i)
The value of x in the vertex of the parabola is: \(x=-\frac{b}{2a}→-3=-\frac{b}{2a}→b=6a\) (ii)
In the point \((-3, 11)\), the value of the \(f(x)\) is 11.
\(f(-3)=11→a(-3)^2+b(-3)+c=11→9a-3b+c=11\) (iii)
Using the first two equation: \(\begin{cases}9a+3b+c=5 \\ 9a-3b+c=11 \end{cases} \)
Equation 1 minus equation 2 is: (i)-(iii) →\(6b=-6→b=-1\) (iv)
Plug in the value of b in the second equation: \9b=6a →a=\frac{b}{6}=-\frac{1}{6}\)
Plug in the values of a and be in the first equation. Then:
\(9(-\frac{1}{6})+3(-1)+c=5⇒c=5+3+\frac{9}{6}=\frac{57}{6}=9 \frac{1}{2}\)
The product of a, b and c\(=(-\frac{1}{6})×(-1)×\frac{57}{6}=\frac{57}{36}=\frac{19}{12}\)
College Entrance Tests
The Best Books to Ace the PSAT 10 Math Test
PSAT Math Practice Workbook 2024 The Most Comprehensive Review for the Math Section of the PSAT Test
Related to This Article
More math articles
- How Hard Is the ALEKS Math Test?
- 7 Easy Tips to Make Math Less Complicated
- Top 10 Tips to Create the SAT Math Study Plan
- Triangles
- What Kind of Math Is on the Accuplacer Next-Generation Test?
- 10 Most Common 7th Grade Georgia Milestones Assessment System Math Questions
- 5 Best Algebra 2 Books for High School Students
- How to Transform Linear Functions
- Top 10 5th Grade OST Math Practice Questions
- CLEP College Math FREE Sample Practice Questions
What people say about "Full-Length PSAT 10 Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.