How to Graph the Secant Function?

A step-by-step guide to graphing the secant function

The secant function is periodic in trigonometry. The secant function can be defined as the ratio of the length of the hypotenuse to the length of the base in a right triangle. It is the reciprocal of the \(cos\) function and is also written as \(sec x = \frac{1}{cos x}\).

Graphing the secant becomes very easy because we already know the cosine graph, so we can easily derive the graph for \(sec x\) by finding the reciprocal of each \(cos\) value. When the value of \(cos x\) is very small, the value of \(sec x\) will be very large. That is, finding \(\frac{1}{y}\) for each value of \(y\) in the curve \(y= cos x\). The table below shows some angles in radians:

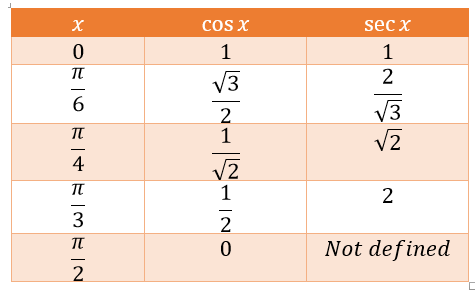
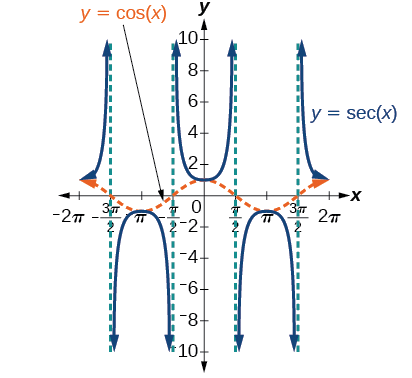
We also see that when the value of the \(cos\) function is zero, the secant function goes to infinity, which means that when the cosine value is \(0\), the secant is undefined. So we get the \(sec x\) graph below: