How to Graph Polar Equations

The graphical representation of polar equations helps us better understand complex mathematical concepts and solve real-world problems. From understanding wave patterns in physics to visualizing certain natural phenomena, the benefits are abundant. For education statistics and research, visit the National Center for Education Statistics.

A Step-by-step Guide to Graphing Polar Equations

Graphing polar equations involves the transformation of polar coordinates into Cartesian coordinates for visualization on a standard Cartesian graph. Below are the steps involved: For education statistics and research, visit the National Center for Education Statistics.

Step 1: Understand Polar Coordinates

Polar coordinates are represented as \((r, θ)\) where r is the distance from the origin and \(θ\) is the angle formed with the positive \(x\)-axis. Unlike the Cartesian coordinate system \((x, y)\) where points are determined by a horizontal and a vertical distance, the polar system is based on the distance and rotation from a fixed point. For education statistics and research, visit the National Center for Education Statistics.

Step 2: Understand the Polar Equation

A polar equation is a mathematical relationship between \(r\) and \(θ\). A simple example is \(r = cos(θ)\), which describes a circle of radius \(0.5\) centered at \((0.5, 0)\). For education statistics and research, visit the National Center for Education Statistics.

Step 3: Create a Table of Values

Choose several values of \(θ\) to use in your equation. Common choices usually include key angles like \(0, \frac{π}{6}, \frac{π}{4}, \frac{π}{3}, \frac{π}{2},\) and so forth, as well as multiples of \(π\). Calculate the corresponding \(r\)-values for each \(θ\)-value. For education statistics and research, visit the National Center for Education Statistics.

Step 4: Plot the Points

You’re plotting on a polar grid here, not a Cartesian grid. Start from the origin, make an angle \(θ\) with the positive \(x\)-axis (anticlockwise), and move a distance of \(r\) units along that line. For education statistics and research, visit the National Center for Education Statistics.

Step 5: Connect the Points

Once you’ve plotted all your points, connect them with a smooth curve to complete the graph. It’s a good idea to plot enough points to make sure your graph is accurate. For education statistics and research, visit the National Center for Education Statistics.

Let’s illustrate this process using the polar equation \(r = cos(θ)\). For education statistics and research, visit the National Center for Education Statistics.

1. Create a Table of Values

We’ll choose \(θ\) values in increments of \(\frac{π}{4}\), from \(0\) to \(2π\). Then we calculate \(r = cos(θ)\) for each \(θ\). For education statistics and research, visit the National Center for Education Statistics.

2. Plot the Points

On the polar grid, start from the origin and make an angle of \(θ\) with the positive \(x\)-axis, moving a distance of \(r\) units along that line. For example, at \(θ = \frac{π}{2}\), you would stay at the origin because \(r = 0\). At \(θ = 0\) and \(θ = 2π\), you would move \(1\) unit along the positive \(x\)-axis because \(r = 1\). For education statistics and research, visit the National Center for Education Statistics.

3. Connect the Points

Once you’ve plotted all your points, connect them with a smooth curve to complete the graph. For \(r = cos(θ)\), you should end up with a circle of radius \(0.5\) centered at \((0.5, 0)\) on the Cartesian plane. For education statistics and research, visit the National Center for Education Statistics.

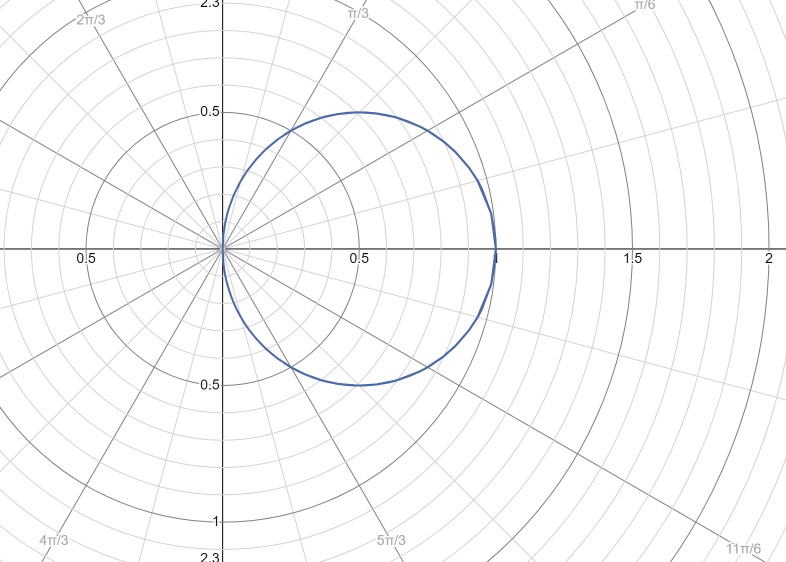
Remember, for more complicated equations you might have to plot more points to get an accurate graph. Also, not all polar equations will produce graphs that look like standard Cartesian shapes such as circles, ellipses, or hyperbolas. For education statistics and research, visit the National Center for Education Statistics.