What Is a Monomial?

Monomials are the building blocks of polynomials and are called terms when they are part of larger polynomials. In other words, each term in a polynomial is a monomial.

Related Topics

• How to Multiply and Divide Monomials
• How to Multiply a Polynomial and a Monomial

A step-by-step guide to monomial

A monomial is defined as a phrase that has a single non-zero term. It consists of different parts such as variables, coefficients, and degrees. The variables in a monomial are the letters in it.

Coefficients are numbers that are multiplied by the variables of the monomial. The degree of a monomial is the sum of the exponents of all the variables. 

How to find a monomial?

A monomial can be easily identified with the help of the following properties:

• A monomial expression must have a single non-zero term.
• The exponents of the variables must be non-negative integers.
• There should not be any variable in the denominator.

How to find a degree of a monomial?

The degree of a monomial is the sum of the exponents of all the variables. It is always a non-negative integer. For example, the degree of the monomial \(abc^2\) is \(4\). The exponent of the variable \(a\) is \(1\), the exponent of variable \(b\) is \(1\), and the exponent of variable \(c\) is \(2\). Adding all these exponents, we get, \(1+1+2=4\).

How to Factor Monomials?

When factoring monomials, we always factor in coefficients and variables separately. Factoring a monomial is as simple as factoring a whole number.

In the same way, we can factorize a monomial. We just have to remember that we always factorize coefficients and variables separately.

Example: Factorize the monomial, \(15y^3\).

Solution:

In the given monomial, \(15\) is the coefficient, and \(y^3\) is the variable.

• The prime factors of the coefficient,\(15\), are \(3\) and \(5\).
• The variable \(y^3\) can be factored in as \(y×y× y\).
• Therefore, the complete factorization of the monomial is \(15y^3 = 3 × 5 × y × y × y\).

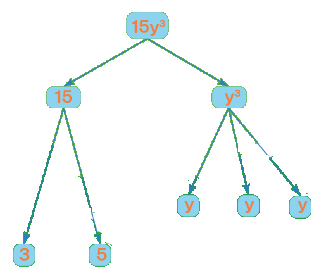
Monomial – Example 1:

 Is \(\frac{14z}{x}\) a monomial expression?

Solution:

The expression has a single non-zero term, but the denominator of the expression is variable. Therefore, the expression \(\frac{14z}{x}\) is not a monomial.

Exercises for Monomial

Factor each of the following monomials.

1. \(\color{blue}{10x^2}\)
2. \(\color{blue}{8 x^2 y^2}\)
3. \(\color{blue}{18 x y}\)

1. \(\color{blue}{2. 5. x. x}\)
2. \(\color{blue}{2. 2. 2. x. x. y. y}\)
3. \(\color{blue}{2. 3. 3. x. y}\)