How to Graph the Cosecant Function?
The cosecant function is the reciprocal of the trigonometric function sine. In this guide, you will learn more about the graph of the cosecant function.
Tutor-style math help
Graph the Cosecant Function: what to notice and how to work it
Trigonometry skill
Secant and cosecant graphs are reciprocal trig graphs. Their asymptotes happen where the matching cosine or sine graph equals zero.
What to notice first
Graph the related sine or cosine guide curve first, then place secant or cosecant branches around the guide curve's peaks and zeros.
Common student mistake
Do not draw secant or cosecant as a regular sine wave. These reciprocal graphs have vertical asymptotes and separated U-shaped branches.
Key formulas and cues
\(\sec x=\frac{1}{\cos x}\)
\(\csc x=\frac{1}{\sin x}\)
\(\cos x=0\Rightarrow\sec x\text{ asymptote}\)
\(\sin x=0\Rightarrow\csc x\text{ asymptote}\)
A reliable path
- Choose the modelUse a right triangle, the unit circle, or a transformed graph.
- Track unitsConvert degrees and radians when needed.
- Use identitiesReplace complicated trig expressions with equivalent simpler ones.
Worked examples
Find secant asymptotes
Example: Where does \(y=\sec x\) have asymptotes?
- Secant is 1/cosine.
- Asymptotes occur where cosine is 0.
- Cosine is 0 at pi/2 plus multiples of pi.
Answer: \(x=\frac{\pi}{2}+k\pi\).
Find cosecant asymptotes
Example: Where does \(y=\csc x\) have asymptotes?
- Cosecant is 1/sine.
- Asymptotes occur where sine is 0.
- Sine is 0 at multiples of pi.
Answer: \(x=k\pi\).
Try one before moving on
Try: Where does \(y=\sec x\) have asymptotes between \(0\) and \(2\pi\)?
Answer: \(x=\pi/2\) and \(x=3\pi/2\).
Next step: do the matching worksheet or quiz while the method is still fresh, then come back and explain the first step in your own words.
x
Graph the Cosecant Function: pop-up practice
Answer these quick questions, then use the feedback to decide which part of the lesson to review.
Choose an answer to begin.
1. \(\sec x\) is the reciprocal of:
2. \(\csc x\) has asymptotes where:
3. Secant and cosecant graphs have:
A step-by-step guide to graphing the cosecant function
The cosecant function is the reciprocal of the trigonometric function \(sin\). Since the cosecant function is the reciprocal of the \(sin\) function, we can write its formula as:
\(\color{blue}{csc (\theta)=\frac{Hypotenuse}{opposite\: side}=\frac{1}{sin\:\theta}}\)
\(cosec x\) is defined for all real numbers except for values where \(sin x\) is equal to zero. Therefore, we have vertical asymptotes at points where \(csc x\) is not defined. Also, using the values of \(sin x\), we have \(y=csc x\) as:
- When \(x = 0\), \(sin x = 0\) \(\rightarrow\) \(csc x =\) not defined
- When \(x = \frac{\pi }{6}\), \(sin x = \frac{1}{2}\)\(\rightarrow\) \(csc x = 2\)
- When \(x =\frac{\pi }{4}\), \(sin x=\frac{1}{\sqrt{2}}\)\(\rightarrow\) \(csc x = \sqrt{2}\)
- When \(x =\frac{\pi }{3}\), \(sin x= \frac{\sqrt{3}}{2}\)\(\rightarrow\) \(csc x = \frac{2}{\sqrt{3}}\)
- When \(x =\frac{\pi }{2}\), \(sin x = 1\)\(\rightarrow\) \(csc x=1\)
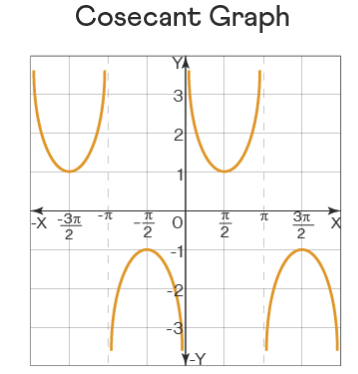
Therefore, by drawing the above points on a graph and connecting them, we have the cosecant graph as follows:
Original price was: $109.99.$54.99Current price is: $54.99.
Original price was: $109.99.$54.99Current price is: $54.99.
Related to This Article
More math articles
- Getting a Math Degree: Hacks to Make Your Life Easier
- Top 10 SAT Math Prep Books (Our 2026 Favorite Picks)
- Indiana ILEARN Grade 7 Math Worksheets: 95 Free Printable PDFs with Answer Keys
- Algebra 1 Worksheets: FREE & Printable
- Coattail effects
- Pennsylvania PSSA Grade 5 Math Worksheets — 49 Free Printable Single-Skill PDFs
- How to Factor Polynomials?
- How to Find Complex Roots of the Quadratic Equation?
- The Best Grade 8 ELA Practice Tests for Delaware Students
- OAR Math Practice Test Questions
What people say about "How to Graph the Cosecant Function? - Effortless Math"?
No one replied yet.