Finding Derivatives Made Easy! Power Rule of Differentiation
The power rule for derivatives is a key concept in calculus, enabling easy calculation of derivatives for functions with powers, greatly simplifying the process. It is one of the most important and frequently used rules of derivatives.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"] [include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Power rule has been explained briefly under “rules of differentiation”.
Introduction and derivative of \( x\):
Power rule states that when you want to find the derivative of a powered variable, the exponent comes down to be the coefficient of the variable, then for the new exponent of variable, we take the previous exponent of the variable and subtract it by \( 1 \)
In mathematical terms: if \( f(x)=x^n \), then: \( f'(x) = nx^{n-1} \)
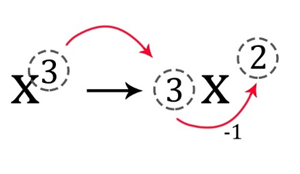
If the variable had a coefficient, it will be multiplied by the result. For example:
\( f(x) = 3x^{1/2} \Rightarrow f'(x) = \frac{1}{2} \cdot 3x^{1/2 – 1} = \frac{3}{2}x^{-1/2} = \frac{3}{2\sqrt{x}} \)
\( f(x) = 3x^{-2} \Rightarrow f'(x) = -2 \cdot 3x^{-2 – 1} = -6x^{-3} = -\frac{6}{x^3} \)
Derivative of \( f(x) \):
If instead of a single variable, we had a function \( f(x) \) that was powered, we need to take this into account, and first, find the derivative like we normally would do (if we were dealing with a simple variable), then multiply the result by the derivative of that function. For example, if the problem was \( (3x)^(-2) \), to find its derivative:
\( f(x) = (3x)^{-2} \Rightarrow f'(x) = -2 \cdot (3x)^{-2 – 1} \cdot 3 = -6(3x)^{-3} = -\frac{6}{(3x)^3} \)
You can see we get the same result if we simplify the exponent first:
\( f(x) = (3x)^{-2} = \frac{1}{9x^2} \Rightarrow f'(x) = -2 \cdot \frac{1}{9} \cdot x^{-3} = -\frac{2}{9x^3} \)
Another thing to remember, we can convert some radicals into a powered function/variable, and solve the radical using power rule. Because another way of writing a radical, is to remove the radical and set the exponent of the variable that was under the radical, as: \(\frac{exponent of variable}{radical index}
For example, \( \sqrt{x} = x^{1/2} \)
\( \sqrt[3]{x^2} = x^{2/3} \)
And so on. So: \( f(x) = x^{2/3} \)
\( f'(x) = \frac{2}{3} \cdot x^{2/3 – 1} = \frac{2}{3} \cdot x^{-1/3} = \frac{2}{3x^{1/3}} \)
Related to This Article
More math articles
- Using Decimals and Fractions to Solve One-Step Addition and Subtraction
- FREE 6th Grade NYSE Math Practice Test
- p-Series in Infinite Sums: Convergence Test Simplified
- 7th Grade IAR Math Practice Test Questions
- How to Find Factors of Numbers?
- What Level of Math is Tested on the PSAT/NMSQT?
- The Best ACT Math Worksheets: FREE & Printable
- Long Division using 1 Number
- What Kind of Math Is on the ACT Test?
- How to Solve Permutations and Combinations? (+FREE Worksheet!)
What people say about "Finding Derivatives Made Easy! Power Rule of Differentiation - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.