FREE AFOQT Math Practice Test

Welcome to our FREE AFOQT Math practice test, with answer key and answer explanations. This practice test’s realistic format and high-quality practice questions can help you succeed on the AFOQT Math test. Not only does the test closely match what you will see on the real AFOQT Mathematics, but it also comes with detailed answer explanations.

For this practice test, we’ve selected 20 real questions from past exams for your AFOQT Mathematics Practice test. You will have the chance to try out the most common AFOQT Math questions. For every question, there is an in-depth explanation of how to solve the question and how to avoid mistakes next time.

Use our free AFOQT Math practice tests and study resources (updated for 2022) to ace the AFOQT Math test! Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the AFOQT Math Test

10 Sample AFOQT Math Practice Questions

1- A football team had $20,000 to spend on supplies. The team spent $14,000 on new balls. New sports shoes cost $120 each. Which of the following inequalities represent the number of new shoes the team can purchase.

A. \(120x+14,000 (\leq ) 20,000\)

B. \(20x+14,000 (\geq ) 20,000\)

C. \(14,000x+120 (\leq ) 20,000\)

D. \(14,000x+12,0 (\geq ) 20,000\)

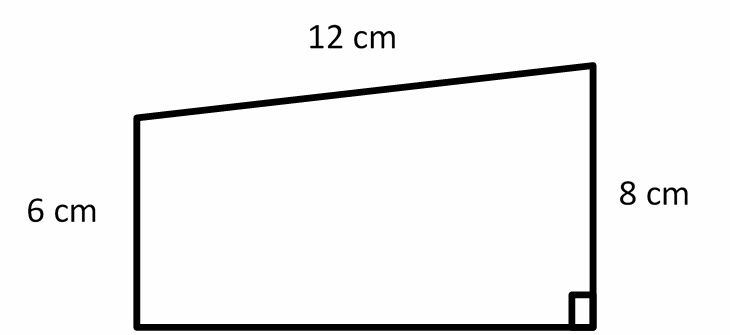
2-The perimeter of the trapezoid below is 36 cm. What is its area?

A. \(576 cm^2\)

B. \(70 cm^2\)

C. \(48 cm^2\)

D. \(24 cm^2\)

3- A bank is offering \(3.5\%\) simple interest on a savings account. If you deposit $12,000, how much interest will you earn in two years?

A. \($420\)

B. \($840\)

C. \($4200\)

D.\($8400\)

4- Which of the following graphs represents the compound inequality \(-2{\leq}2x-4<8\)?

A.

B.

C.

D.

5- Last week \(24,000\) fans attended a football match. This week three times as many bought tickets, but one-sixth of them canceled their tickets. How many are attending this week?

A.\(48,000\)

B. \(54,000\)

C.\(60,000\)

D. \(72,000\)

6- In the \(xy\)-plane, the point \(4,3\) and \(3,2\) are on line A. Which of the following points could also be on line A?

A. (-1, 2)

B. (5, 7)

C. (3, 4)

D. (-1, -2)

7- What is the equivalent temperature of \(104^{\circ}\) F in Celsius?
C = \(\frac{5}{9}\) F \(- 32\)

A. 32

B. 40

C. 48

D. 52

8- If \(150\%\) of a number is 75, then what is the \(90\%\) of that number?

A. 45

B. 50

C. 70

D. 85

9- Simplify the expression:
\((6x^3-8x^2+2x^4 )-(4x^2-2x^4+2x^3 )\)

A. \(4x^3-12x^2\)

B. \(4x^4+4x^3-12x^2\)

C. \(8x^3-12x^2\)

D. \(x^4+4x^3-12x^2\)

10- In two successive years, the population of a town is increased by \(15\%\) and \(20\%\). What percent of the population is increased after two years?

A. \(32\%\)

B. \(35\%\)

C. \(38\%\)

D. \(68\%\)

11- A shirt costing $200 is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt?

A. (200) (0.70)

B. (200) – 200 (0.30)

C. (200) (0.15) – (200) (0.15)

D. (200) (0.85) (0.85)

12- In a stadium, the ratio of home fans to visiting fans in a crowd is 5:7. Which of the following could be the total number of fans in the stadium?

A. 12,324

B. 42,326

C. 44,566

D. 66,812

13- In a classroom of 60 students, 42 are female. What percentage of the class is male?

A. \(34\%\)

B. \(22\%\)

C. \(30\%\)

D.  \(26\%\)

14- Which of the following points lies on the line \(x+2y=4\)?

A. (-2, 3)

B. (1, 2)

C. (–1, 3)

D.  (-3, 4)

15- During the last week of track training, Emma achieves the following times in seconds: 66, 57, 54, 64, 57, and 59. Her three best times this week (least times) are averaged for her final score on the course. What is her final score?

A. 56 seconds

B. 57 seconds

C. 59 seconds

D. 61 seconds

16- 5 less than twice a positive integer is 83. What is the integer?

A. 39

B. 41

C. 42

D. 44

17- How many square feet of tile is needed for a 15 feet \(x\) 15 feet room?

A. 225 square feet

B. 118.5 square feet

C. 112 square feet

D. 60 square feet

18- 11 yards 6 feet and 4 inches equal to how many inches?

A. 388

B. 468

C. 472

D. 476

19- Mr. Carlos’s family is choosing a menu for their reception. They have 3 choices of appetizers, 5 choices of entrees, 4 choices of cake. How many different menu combinations are possible for them to choose from?

A. 12

B. 32

C. 60

D. 120

20- The average of five consecutive numbers is 38. What is the smallest number?

A. 38

B. 36

C. 34

D. 12

Best AFOQT Math Prep Resource for 2022

Answers:

2- B
The perimeter of the trapezoid is \(36 cm\).
Therefore, the missing side (height) is =\( 36 – 8 – 12 – 6 = 10\)
Area of a trapezoid: \(A = \frac{1}{2} h ({b_{1} + b_{2}}) = \frac{1}{2} (10) (6 + 8) = 70\)

3- B
Use simple interest formula:
\(I=prt\)
\((I = interest, p = principal, r = rate, t = time)\)
\(=(12000)(0.035)(2)=840\)

4- D
Solve for \(x\).
\(-2 {\leq} 2x-4 < 8 ⇒\) (add 4 all sides) \(-2+4 {\leq} 2x-4+4 < 8+4 {\Rightarrow}\)
\(2{\leq}2x<12 {\Rightarrow}\) (divide all sides by 2) \(1 {\leq}x < 6\)
\(x\) is between \(1\) and \(6\).

5- C
Three times of \(24,000\) is \(72,000\). One-sixth of them canceled their tickets.
One sixth of \972,000\) equals \(12,000\) \((\frac{1}{6}\) \(\times\) \(72000\) = \(12000)\).
\(60,000\) \((72000 – 12000 = 60000)\) fans are attending this week

6- D
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and b is the y-intercept of the line.
Two points \(4,3\) and \(3,2\) are on line A. Therefore, the slope of the line A is:
slope of line \(A=\frac{(y_2- y_1)}{(x_2 – x_1) } =\frac{2-3}{3-4} = \frac{-1}{-1}\)
The slope of line A is 1. Thus, the formula of the line A is:
\(y=mx+b=x+b\), choose a point and plug in the values of x and y in the equation to solve for b. Let’s choose point \(4, 3\). Then:
\(y=x+b\)\(\rightarrow\)\(3=4+b\)\(\rightarrow\)\(b=3-4=-1\)
The equation of line A is: \(y=x-1\)
Now, let’s review the choices provided:
A. \((-1,2)\) \(y=x-1\)\(\rightarrow\)\(2=-1-1=-2\) (This is not true.)
B. \((5,7)\) \(y=x-1\)\(\rightarrow\)\(7=5-1=4\) (This is not true.)
C. \((3,4)\) \(y=x-1\)\(\rightarrow\)\(4=3-1=2\) (This is not true.)
D. \((-1,-2)\) \(y=x-1\)\(\rightarrow\)\(-2=-1-1=-2\) (This is true!)

7- B
Plug in 104 for F and then solve for C.
\(C = \frac{5}{6} (F – 32) {\Rightarrow} C = \frac{5}{9} (104 – 32) {\Rightarrow} C = \frac{5}{9} (72) = 40\)

8- A
First, find the number.
Let \(x\) be the number. Write the equation and solve for \(x\).
\(150\%\) of a number is 75, then:
\(1.5{\times}x=75 {\Rightarrow} x=75{\div}1.5=50\)
\(90\%\) of 50 is:
\(0.9 {\times} 50 = 45\)

9- B
Simplify and combine like terms.
\((6x^3-8x^2+2x^4 )-(4x^2-2x^4+2x^3 ) {\Rightarrow} (6x^3-8x^2+2x^4 )-4x^2+2x^4-2x^3 {\Rightarrow}
4x^4+4x^3-12x^2\)

10- C
the population is increased by \(15\%\) and \(20\%\).
\(15\%\) increase changes the population to \(115\%\) of original population.
For the second increase, multiply the result by \(120\%\).
\((1.15)\) \(\times\) \((1.20)\) = \(1.38\) = \(138\%\)
38 percent of the population is increased after two years.

11- C
To find the discount, multiply the number by \(100{%} –\) rate of discount.
Therefore, for the first discount we get: \(200\) \(100{%} – 15{%}\) = \(200\) \(0.85\) = \(170\)
For the next 15{%} discount: \(200\) \(0.85\) \(0.85\)

12- A
In the stadium, the ratio of home fans to visiting fans in a crowd is 5:7. Therefore, total number of fans must be divisible by \(12: 5 + 7 = 12\).
Let’s review the choices:
A. \(12,324: 12,324 (\div ) 12 = 1027\)
B. \(42,326 42,326 (\div ) 12 = 3,527.166\)
C. \(44,566 44,566 (\div ) 12 = 3,713.833\)
D. \(66,812 66,812 (\div ) 12 = 5,567.666\)
Only choice A when divided by 12 results a whole number.

13- C
\(60 – 42 = 18\) male students
\(\frac{18}{60} = 0.3 \)
Change 0.3 to percent ⇒\(0.3 × 100\) =\(30\%\)

14- A
\((x+2y=4)\). Plug in the values of x and y from choices provided. Then:
A. \(-2,3\) \(x+2y=4\)\(\rightarrow \)\(-2+2(3)=4\)\(\rightarrow \)\(-2+6=4\) (This is true!)
B. \((1,2)\) \(x+2y=4\)\(\rightarrow\)\(1+2(2)=4\)\(\rightarrow\)\(1+4=4\) (This is NOT true!)
C. \((-1,3)\) \(x+2y=4\)\(\rightarrow \)\(-1+2(3)=4\)\(\rightarrow\)\(-1+6=4\) (This is NOT true!)
D. \((-3,4)\) \(x+2y=4\)\(\rightarrow\)\(-3+2(4)=4\)\(\rightarrow\)\(-3+8=4\) (This is NOT true!)

15- A
Emma’s three best times are 54, 57, and 57.
The average of these numbers is:
average \(=\frac{sum}{total}\)
Sum \(= 54 + 57 + 57 = 168\)
Total number of numbers = 3
average \(=\frac{168}{3}=56\)

16- D
Let \(x\) be the integer. Then:
\(2x – 5 = 83\)
Add 5 both sides: \(2x = 88\)
Divide both sides by 2:\( x = 44\)

17- A
The area of a 15 feet\(x\) 15 feet room is 225 square feet.
\(15 × 15 = 225\)

18- C
\(11 \times 36 + 6 \times 12 + 4 = 47\)

19- C
To find the number of possible outfit combinations, multiply number of options for each factor:
\(3\) \(\times\) \(5\) \(\times\) \(4 = 60\)

20- B
Let \(x\) be the smallest number. Then, these are the numbers:
\( x, x+1, x+2, x+3, x+4 \)
average =\(\frac{sum of terms}{number of terms} \Rightarrow 38 = \frac{x+(x+1)+(x+2)+(x+3)+(x+4)}{5} \Rightarrow 38= \frac{5x+10}{5} \Rightarrow 190 = 5x+10 \Rightarrow 180 = 5x \Rightarrow x=36\)

Looking for the best resource to help you succeed on the AFOQT Math test?

The Best Books to Ace the AFOQT Math Test

More from Effortless Math for AFOQT Test …

Use our Full-Length AFOQT Math Practice Test to improve your AFOQT Math score.

We have prepared a complete list of AFOQT Math formulas to review the most common formulas.

If you can’t attend AFOQT Math preparation classes in person here are the top free AFOQT practice test websites for you: Top 10 Websites for FREE AFOQT Math Preparation.

The Perfect Prep Books for the AFOQT Math Test

Have any questions about the AFOQT Test?

Write your questions about the AFOQT or any other topics below and we’ll reply!