How to Find Complementary, Supplementary, Vertical, Adjacent, and Congruent Angles?
TL;DR: Five angle relationships do most of the work in geometry. Complementary angles add up to 90 degrees. Supplementary ones add up to 180. Vertical angles, the pair sitting across from each other where two lines cross, are always equal. Adjacent angles share a vertex and a side without overlapping. And congruent angles? They simply have the same measure. Learn these five definitions and you've got the vocabulary you need to handle almost every angle problem you'll meet.
Key takeaways:
- Complementary: two angles whose measures add to \(90^\circ\).
- Supplementary: two angles whose measures add to \(180^\circ\).
- Vertical angles: opposite angles formed by intersecting lines - always congruent.
- Adjacent angles: share a common vertex and a common side, no overlap.
- Congruent angles: have equal measures - written with the symbol \(\cong\).
When angles appear in groups of two to indicate a particular geometric property, they are called pairs of angles. In this article, you will be familiar with the types of pairs of angles.
When angles appear in groups of two to display a certain geometrical property they are called angle pairs. There is a special relationship between pairs of angles. Some of the angle pairs contain complementary angles, supplementary angles, vertical angles, and adjacent angles.
Related Topics
A step-by-step guide to finding complementary, supplementary, vertical, adjacent, and congruent angles
When two angles are paired, then there exist different angles such as:
1. Complementary angles
If the sum of the two angles reaches \(90\) degrees, they are called complementary angles. In other words, when the complementary angles are placed together, they form a right angle (\(90\) degrees).
Each angle between the complementary angles is called the “complement” of the other angle.
2. Supplementary angles
When the sum of the two angles is \(180\) degrees, they are called supplementary angles. The two angles when added make up \(180°\). For example, \(110°\) and \(70°\) make up \(180°\). So these two angles are said to be supplementary. Here, one angle is the supplement of another angle. For example, the supplement of \(60°\) is \((180° – 60°)\), which is \(120°\).
3. Vertical angles
Vertical angles are a pair of non-adjacent angles formed by the intersection of two straight lines. In simple words, vertical angles are located across from one another in the corners of the \(“X”\) formed by two straight lines. They are also called vertically opposite angles as they are situated opposite each other.
4. Adjacent angles
Two angles are called adjacent angles if they have a common vertex, a common side, and no overlap.
Congruent angles
The definition of congruent angles is “angles that are equal in the measure are known as congruent angles”. In other words, equal angles are congruent angles. It is denoted by the symbol \(“≅”\), so if we want to represent \(∠A\) as congruent to \(∠X\), we will write it as \(∠A ≅ ∠X\).
In the image above, both angles are equal in measurement (\(60^∘\) each). They can completely overlap each other. So, as per the definition, we can say that both the given angles are congruent.
Finding Complementary, Supplementary, Vertical, Adjacent, and Congruent Angles – Example 1:
Find the angle \(x\) in the following figure.
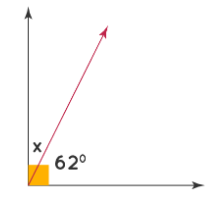
Solution:
In the given figure, \(x\) and \(62°\) are complementary angles as they form a right angle. Hence, their sum is 90°.
\(x + 62° = 90°\)
\(x = 90°-62°\)
Therefore, the value of angle \(x\) is \(28°\).
Exercises for Finding Complementary, Supplementary, Vertical, Adjacent, and Congruent Angles
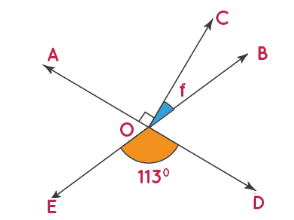
- Find the measurement of angle \(f\).
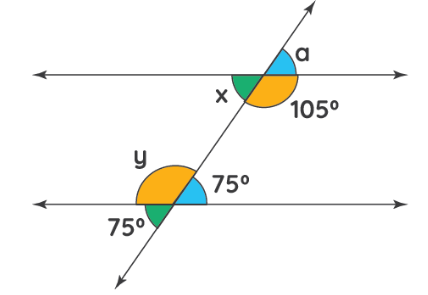
- Find the measures of angles \(x\), \(y\), and \(a\) in the figure.
- \(\color{blue}{23°}\)
- \(\color{blue}{∠x = 75°, ∠y = 105°, ∠a =75°}\)
Recommended EffortlessMath Books
For a deeper walk through every geometry skill from the ground up, Geometry for Beginners covers angles, area, volume, triangles, and transformations with worked examples and plenty of practice. For algebra-heavy geometry topics, the companion Algebra I for Beginners ties the coordinate-plane work back to linear equations.
Frequently Asked Questions
What are complementary angles?
Two angles whose measures add up to exactly \(90^\circ\). If one angle is \(35^\circ\), its complement is \(90 – 35 = 55^\circ\). Complementary angles don’t have to be adjacent – they just have to sum to \(90^\circ\). Remember: “C” for complementary, “C” for corner (a right angle).
What are supplementary angles?
Two angles whose measures add up to exactly \(180^\circ\). If one is \(110^\circ\), its supplement is \(70^\circ\). Supplementary angles often form a straight line when adjacent, but they don’t have to be drawn together – just summing to \(180^\circ\) is enough. “S” for supplementary, “S” for straight line.
What are vertical angles?
When two straight lines cross, they form four angles. The pairs of angles opposite each other (not adjacent) are vertical angles – and they’re always equal. If one is \(40^\circ\), the angle opposite is also \(40^\circ\). The two angles next to it (which form straight lines with the original) are \(140^\circ\) each.
What are adjacent angles?
Two angles that share a common vertex and a common side, with no overlap. They sit next to each other. Adjacent angles can be complementary, supplementary, or neither – it just depends on their measures. The key feature is the shared vertex and side.
What are congruent angles?
Angles that have the same measure. Two angles of \(45^\circ\) each are congruent. The notation is \(\angle A \cong \angle B\), read “angle A is congruent to angle B.” Vertical angles are always congruent; corresponding angles in similar figures are congruent; angles cut by a transversal in parallel lines are often congruent.
How do I tell if two angles are complementary or supplementary?
Add their measures. If the sum is \(90^\circ\), they’re complementary. If the sum is \(180^\circ\), they’re supplementary. If neither, they’re just two angles with no special relationship. The angles don’t even need to be touching – the relationship is about their sum, not their position.
Walk me through an example.
Two angles are supplementary, and one is twice the other. Find both. Let the smaller be \(x\); the larger is \(2x\). Their sum is \(180^\circ\), so \(x + 2x = 180\), \(3x = 180\), \(x = 60\). The two angles are \(60^\circ\) and \(120^\circ\). Check: \(60 + 120 = 180\) ✓.
What if angles are given as expressions, not numbers?
Treat them like algebra. If two vertical angles are \(2x + 10\) and \(4x – 30\), set them equal: \(2x + 10 = 4x – 30\). Solve: \(40 = 2x\), \(x = 20\). Substitute back: both angles are \(50^\circ\). This is a common pattern on tests.
Can three angles be complementary?
By strict definition, complementary refers to PAIRS that add to \(90^\circ\). Three or more angles that sum to \(90^\circ\) aren’t typically called complementary. Same with supplementary – it’s a two-angle relationship. For three or more, you’d describe them as “angles whose sum is \(90^\circ\)” instead.
Where does this skill show up?
Grade 7-8 state tests, geometry class, SAT, ACT, and most standardized math tests. Common scenarios: find the complement or supplement of a given angle; find vertical angles in a diagram; set up algebra equations from a figure with angle expressions. Master these basic relationships, and most geometry proofs become much easier.
Related EffortlessMath Lessons
If a topic on this page feels rusty, these short lessons go deeper:
Related to This Article
More math articles
- Free Grade 5 Math Practice for Idaho ISAT Fifth Graders: 49 Standards-Aligned Worksheet PDFs
- Top 10 CLEP College Algebra Prep Books (Our 2023 Favorite Picks)
- The Best Grade 4 Math Book for Maine Students
- The World of Separable Differential Equations
- Geometry in Action: Crafting the Circumscribed Circle of a Triangle
- 7th Grade K-PREP Math Worksheets: FREE & Printable
- FREE 8th Grade PARCC Math Practice Test
- Grade 10 Math Worksheets: FREE & Printable
- How to Identify Relations and Functions? (+FREE Worksheet!)
- Overview of the ISEE Lower Level Mathematics Test
What people say about "How to Find Complementary, Supplementary, Vertical, Adjacent, and Congruent Angles? - Effortless Math"?
No one replied yet.