Intelligent Math Puzzle – Challenge 92
Some Math puzzles like the following one stumped even the smartest people. Can You Solve It? The solution is also given.
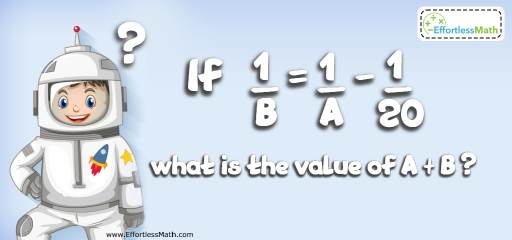
Challenge:
If A and B are integers and \(\frac{1}{B}=\frac{1}{A}-\frac{1}{20}\) what is the value of A+B?
The Absolute Best Book to challenge your Smart Student!

The correct answer is 9.
\(\frac{1}{B} =\frac{1}{A} -\frac{ 1}{20}\)
Therefore, A is less than B. Why?
Plug in different values for A.
Let’s begin with 2. If A \(= 2 → \frac{1}{B} = \frac{ 1}{2} – \frac{ 1}{20} → \frac{ 1}{B} = \frac{ 9}{20} → 9B = 20\)
B is an integer. Therefore, B cannot be \(\frac{ 20}{9}\)
A \(= 3 → \frac{ 1}{B} = \frac{ 1}{3} – \frac{ 1}{20} → \frac{ 1}{B} = \frac{ 17}{60} → 17B = 60\)
A \(= 4 → \frac{ 1}{B} = \frac{ 1}{4} – \frac{ 1}{20} → \frac{ 1}{B} = \frac{4}{20} → 4B = 20 → B = 5\) Bingo!
A = 4 and B = 5 → A + B = 9The Best Books to Ace Algebra
Original price was: $29.99.$14.99Current price is: $14.99.Original price was: $29.99.$14.99Current price is: $14.99.Satisfied 1 StudentsOriginal price was: $24.99.$14.99Current price is: $14.99.Satisfied 92 StudentsOriginal price was: $24.99.$15.99Current price is: $15.99.Satisfied 125 Students
Related to This Article
More math articles
- PSAT 10 Math Worksheets: FREE & Printable
- Is a Calculator Allowed on the CBEST Test?
- CLEP College Math FREE Sample Practice Questions
- What does SAT Stand for?
- How to Solve Word Problems of Volume of Cubes and Rectangular Prisms
- Top Ten Cameras for Classroom Recording
- 6th Grade NHSAS Math Worksheets: FREE & Printable
- Addition of Money Quantities
- How to Find Perimeter and Area Relationship
- How to Solve a Quadratic Equation by Completing the Square?

















What people say about "Intelligent Math Puzzle – Challenge 92 - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.