Geometry Puzzle – Challenge 77
This is a great math puzzle and critical thinking challenge that is sure to get you thinking!
Challenge:
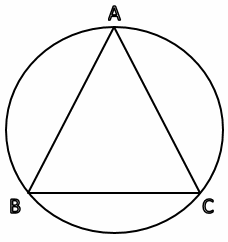
What is the perimeter of the inscribed equilateral triangle, if the diameter of the circle above is 4?
A- \(4\sqrt{2}\)
B- \(4\sqrt{3}\)
C- \(6\sqrt{2}\)
D- \(6\sqrt{3}\)
E- 12
The Absolute Best Book to Challenge Your Smart Student!
Original price was: $16.99.$11.99Current price is: $11.99.
Satisfied 123 Students
The correct answer is D.
Draw the bisector of the angle A perpendicular to line BC.
D is the center of the circle and CD is equal to the radius. The diameter of the circle above is 4. So, CD is 2.
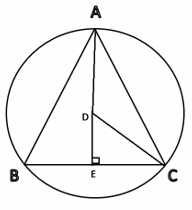
Triangle CDE is a 30-60-90 degree triangle and angle DCE is 30.
Since, CD is 2 (the hypotenuse of the triangle CDE), DE is 1 and CE is \(\sqrt{3}\). Why?
Therefore, BC is \(2\sqrt{3} \) and the perimeter of the triangle ABC is
\(3 × 2\sqrt{3} = 6\sqrt{3}\)
The Best Books to Ace Algebra
Original price was: $29.99.$14.99Current price is: $14.99.
Original price was: $29.99.$14.99Current price is: $14.99.
Satisfied 1 Students
Original price was: $24.99.$14.99Current price is: $14.99.
Satisfied 92 Students
Original price was: $24.99.$15.99Current price is: $15.99.
Satisfied 125 Students
Related to This Article
More math articles
- Top 10 CHSPE Math Practice Questions
- The Ultimate 6th Grade NYSTP Math Course (+FREE Worksheets)
- How to Write a Quadratic Function from Its Vertex and Another Point
- How to Identify Characteristics of Quadratic Functions: Graphs
- How to Understand the Concept of Scale Changes: Area and Perimeter
- 8th Grade M-STEP Math Worksheets: FREE & Printable
- 7th Grade NJSLA Math Worksheets: FREE & Printable
- 8th Grade MAP Math FREE Sample Practice Questions
- How to Solve Word Problems of Counting Bills and Coins
- 8th Grade Ohio’s State Tests Math Worksheets: FREE & Printable
What people say about "Geometry Puzzle – Challenge 77 - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.