Unit Prices with Decimals and Fractions

To identify the total price using unit prices and amounts in fractions and decimals, you have to multiply.
To identify the unit price of an item, you have to divide the cost of a certain number of units of an item by the number of units.
Unit rates are written as a ratio with a denominator of 1.

Step by step guide to problems related to unit prices

Here is a step-by-step guide to solving problems related to unit prices:

1. Identify the unit rate by dividing the cost by the quantity. For example, if a can of soda costs $1.50 and contains 12 ounces, the unit rate is $1.50/12 ounces = $0.125/ounce
2. Compare the unit rates to determine which item is the better deal. For example, if a 16-ounce bag of chips costs $2.00, the unit rate is $2.00/16 ounces = $0.125/ounce. Since this is the same unit rate as the can of soda, the price per ounce is the same for both items.
3. Use the unit rate to find the cost of a specific quantity. For example, if you want to know how much it would cost to buy 24 ounces of the chips, you would multiply the unit rate by the quantity: $0.125/ounce x 24 ounces = $3.00
4. Use the unit rate to find the quantity you can buy for a specific amount of money. For example, if you have $5.00 and you want to know how many ounces of chips you can buy, divide the amount of money by the unit rate: $5.00 ÷ $0.125/ounce = 40 ounces
5. Repeat the steps for other items if you need to compare multiple unit prices.
6. Always check for any discounts or offers before making a purchase.
7. Remember that unit price is a way to compare prices of different items and/or different package sizes. Unit price is not always the final price you pay, so it’s important to check the final price too.

Unit Prices with Decimals and Fractions – Examples 1, 2

Solve the problems according to the list.
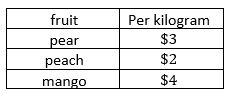
1) Emma went to the store and bought 3 1/4 kilograms of peaches. How much did she spend?

Solutions:
Multiply the price of the peaches per kilogram (2) by the number of kilograms (\(\frac{3 1}{4}\)).
\($2×3 \frac{1}{4}=$2×3.25=6.5$\). So, she spends 6.5$.
2) Jeb went to the store and bought 1.75 kilograms of mangos. How much did he spend?
Solutions:
Multiply the price of the mangos per kilogram (4) by the number of kilograms (0.75)
\($4×1.75=$7\). So, he spends $7.