Theoretical and Empirical Probability Distributions

Experimental probability, also called experimental probability, is the probability that your experiment will give you a particular result. For example, you can toss a coin \(100\) times to see how many heads you get, or you can do a taste test to see if \(100\) people prefer Cola A or Cola B.

You can use this information to make educated guesses (statistics) about what your probabilities would be if you performed the experiments \(1000\), \(10,000\), or even an unlimited number of times. If you do not experiment – if you are just theorizing about it – it is called theoretical probability.

Related Topics

• How to Solve Probability Problems
• How to Find the Probability of an Event

A step-by-step guide to theoretical and empirical probability distributions

Empirical probability formula

Like a mathematical formula, the empirical probability is denoted with the prime notation:

\(\color{blue}{p(A)=\frac{n(A)}{n}}\)

Where:

• \(n(A)\) is the number of times event \(A\) happens
• \(n\) is the number of attempts at the experiment

Experimental vs Empirical vs Relative Frequency

An application like the Relative Frequency Table uses the word “relative frequency” when referring to experimental probability or empirical probability. While the findings of an experiment may be used to calculate experimental probabilities, they can’t be used to calculate their relative frequencies. You may also find experimental probability dubbed “a posteriori” or “frequentist,” but these phrases aren’t used that often.

Different kinds of probabilities:

• Subjective probability: 

When you believe something will happen, you have a subjective probability. This has nothing to do with science. “This scratch-off ticket will be a winner,” or your “hunch” that one cold medicine is better than another, might be the source of your intuitions.

When one person’s subjective probability differs from another’s, it may be exceedingly perplexing. As an example, if you think it’s going to be sunny today, but someone else thinks it’s going to rain, you can’t know for sure.

• Axiomatic probability:

Axiomatic probability is a theory of probability that unifies several different theories. It lays forth a set of principles that apply to all of the above probability classes. When it comes to probabilities, one axiomatic rule is that they are always between \(0\) and \(100\) percent (i.e. from \(0\) to \(1\)).

Theoretical and Empirical Probability Distributions – Example 1:

A survey was conducted to determine the favorite brands of students’ sneakers. Each student chose only one brand from the list of brands \(A\), \(B\), \(C\), \(D\), or \(E\). What is the probability that a student’s favorite sneaker is a \(C\) brand?

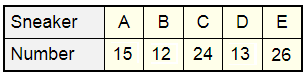
There were \(15 + 12 + 24 + 13 + 26 = 90\) trials in this experiment.

\(24\) out of the \(90\) students chose the brand \(C\).

The probability is :

\(\frac{24}{90}=\frac{4}{15}\)

Theoretical and Empirical Probability Distributions – Example 2:

Find the probability of rolling a \(6\) on a fair die.

No experiment is required. There are \(6\) possible outcomes when rotating the die: \(1\), \(2\), \(3\), \(4\), \(5\), and \(6\).
The only desired result is rolling a \(6\).

The probability is :

\(\frac{1}{6}\)

Exercises for Theoretical and Empirical Probability Distributions

1. In a group of \(50\) people, \(32\) people prefer to order non-vegetarian burgers instead of vegetables. What is the empirical probability that someone will order a vegetable hamburger?
2. At a buffet, \(90\) out of \(100\) people prefer to order coffee instead of tea. What is the empirical probability that someone will order coffee?
3. A bag contains \(6\) blue balls, \(4\) yellow balls, and \(2\) red balls. What is the theoretical probability of getting a yellow ball?
4.  What is the theoretical probability of rolling a \(4\) or a \(7\) with a set of two dice?

1. \(\color{blue}{\frac{9}{25}}\)
2. \(\color{blue}{\frac{1}{10}}\)
3. \(\color{blue}{\frac{4}{12}}\)
4. \(\color{blue}{\frac{1}{4}}\)