Slope Unity in Mean Value Theorem: Average Meets Instant

The Mean Value Theorem states that if a function \( f \) is continuous on a closed interval \([a, b]\) and differentiable on the open interval \((a, b)\), then there exists at least one point \( c \) in \((a, b)\) where the derivative \( f'(c) \) equals the function’s average rate of change over \([a, b]\). This is expressed as \( f'(c) = \frac{f(b) – f(a)}{b – a} \).

here are the steps to find this point on the curve of a function:

1. finding the average rate of change for the interval \( [a,b] \) using the formula \( f'(c) = \frac{f(b) – f(a)}{b – a} \)
2. finding the derivative of the function using rules of differentiation
3. setting the derivative equal to average rate and solving for \( x \), which will be the coordinate of the \( x \) point that we are looking for, and we call it \(c\)

if we want to sketch the secant and tangent lines, here are the steps to do that:

• secant line passes through the first and the last point of the function, so by finding one of these points using \( (x,f(x)) \) for our function, and using point-slope form, (with the slope being average rate of change of the function in the interval), we get the equation for the secant line.

• to find the equation for the tangent line, we put the point that we found in step 3 above using the mean value theorem, into the original function to find the corresponding \( y \) value of that \( x \). using point-slope form for this \( (x,y) \) point with the slope being average rate of change of the function in the interval, we get the equation for the tangent line.

Now let’s apply the Mean Value Theorem to an example: the function \( f(x) = x^3 \) over the interval \( [1, 2] \).

For \( f(x) = x^3 \), we first calculate the average rate of change from \( x = 1 \) to \( x = 2 \):

\( \text{Average rate of change} = \frac{f(2) – f(1)}{2 – 1} = \frac{2^3 – 1^3}{2 – 1} = \frac{8 – 1}{1} = 7 \)

Next, we find the derivative of \( f(x) \):

\( f'(x) = 3x^2 \)

According to the Mean Value Theorem, there exists some \( c \) in the interval \([1, 2]\) such that \( f'(c) = 7 \). So, we set \( f'(c) \) equal to \( 7 \) and solve for \( c \):

\( 3c^2 = 7 \)
\( c^2 = \frac{7}{3} \)
\( c = \sqrt{\frac{7}{3}} \)

Since \(\sqrt{\frac{7}{3}}\) is approximately \( 1.53 \) and lies within the interval \([1, 2]\), it satisfies the conditions of the Mean Value Theorem. Thus, at \( x = \sqrt{\frac{7}{3}} \), the instantaneous rate of change of \( f(x) = x^3 \) equals its average rate of change over the interval \( [1, 2] \).

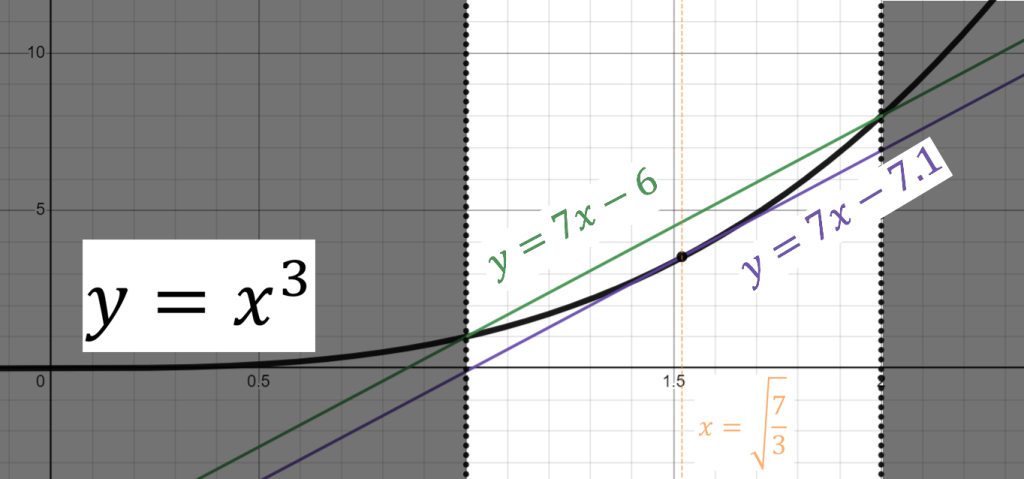
Here, the line \( y=7x-6 \) represents the secant line, connecting the first point of the function on this particular interval, to its last point.

And \( y=7x-7.1 \) is the tangent line, touching the curve \( y=x^3 \) at the point \( \sqrt{\frac{7}{3}} \). this point is the where the average rate of change of the function in the interval \( [1,2] \) is exactly the same as the instantaneous rate of change of \( y=x^3 \).