Slope Fields Simplified: Understanding the Core of Differential Equations

The concept of slope fields, originating in the \(18^th\) century, is attributed to Isaac Newton and Gottfried Wilhelm Leibniz, founders of calculus. Their work laid the groundwork for visualizing differential equations, with slope fields evolving as a critical tool for understanding these equations’ graphical solutions.

How to use slope fields to find the answer to a differential equation:

Understand the Differential Equation:

You should have a first-order differential equation in the form of \(\frac{dy}{dx} = f(x, y)\), where \( y \) is the dependent variable, \( x \) is the independent variable, and \( f(x, y) \) is a function involving both variables.

Determine the Region of Interest:

Identify the region of the \(xy-plane\) where you want to find solutions or where the problem is defined. It’s essential to choose a region that contains the initial conditions (if given) or the range of interest.

Choose Grid Points:

Divide the region of interest into a grid of points. These points will serve as the starting points for drawing line segments that represent the slope of the solution at each point. The grid should be fine enough to capture the behavior of the solutions accurately.

Calculate Slopes:

For each grid point \( (x, y) \), calculate the slope at that point using the differential equation’s right-hand side, \( f(x, y) \). The slope at a particular point is given by the value of \( f(x, y) \) at that point.

Draw Line Segments:

At each grid point, draw a short line segment with a slope equal to the calculated value of \( f(x, y) \). These line segments indicate the direction in which the solution curve would travel at that point.

Connect Line Segments:

Connect the line segments smoothly to form a continuous curve. This curve represents an approximate solution trajectory for the differential equation. You can use the slope field to sketch multiple solution trajectories if needed.

Analyze the Solutions:

Examine the slope field to identify the behavior of the solutions. Look for equilibrium points (where the slopes are zero) and how solutions approach or diverge from these points. You can also identify trends, such as where the solutions are increasing or decreasing.

Incorporate Initial Conditions:

If you have initial conditions (e.g., \( y(x0) = y0 \)), you can use the slope field to estimate the behavior of the solution that passes through that point. Follow the direction of the slope field to trace the solution curve from the initial condition.

Refine and Repeat:

If necessary, refine your slope field by adding more grid points or extending the region of interest to improve the accuracy of your approximate solutions.

Analyze Numerically:

For more precise solutions, you may need to use numerical methods (e.g., Euler’s method, Runge-Kutta methods) to find specific values of the solution at desired points.

Example:

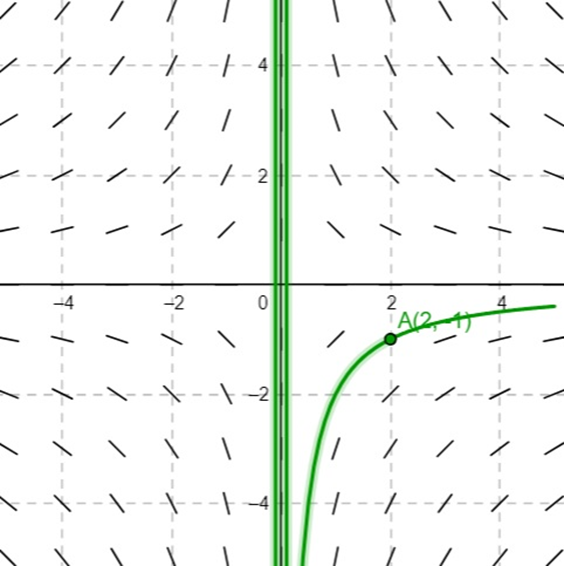
Consider the first-order differential equation:

\(\frac{dy}{dx} = -\frac{y}{x}\)

1. Create a slope field for this differential equation in the region \(1 \leq x \leq 5\) and \(1 \leq y \leq 5\).
2. Use the slope field to sketch the approximate solution curve that passes through the point \((2, 2)\).
3. Determine the behavior of the solution as \(x\) approaches \(0\).

Solution:

To create the slope field, follow these steps:

1. Determine the region of interest in the \((x, y)\) plane.
2. Choose a grid of points in this region.
3. Calculate the slopes at each grid point using the differential equation.
4. Draw short line segments at each point to represent the slopes.
5. Connect these line segments to visualize the solution trajectories.

Using the slope field, sketch the approximate solution curve that passes through the point \((2, 2)\).

Behavior as \(x\) approaches \(0\):

Analyze the behavior of the solution as \(x\) approaches \(0\) based on your slope field and solution curve.

Frequently Asked Questions

What is a slope field?

A slope field, also called a direction field, is a grid of short line segments that shows the slope of a differential equation dy/dx = f(x, y) at many points. Each segment has slope equal to f(x, y) at its point. Solution curves follow the segments, so you can see how solutions behave without solving the equation by algebra.

What is the formula for a slope field?

There is no separate formula: the differential equation itself gives every slope. For dy/dx = f(x, y), plug each grid point into f. With dy/dx = x + y, the point (1, 2) gets a segment with slope 3, and the point (−1, 1) gets a horizontal segment because −1 + 1 = 0. Repeat across the grid and the pattern appears.

What is an example of a slope field?

Take dy/dx = x. The slope depends only on x, so every segment in a vertical column is parallel: flat along x = 0, slope 2 along x = 2, slope −2 along x = −2. The curves that follow these segments are the parabolas y = x²/2 + C. For dy/dx = y, slopes depend only on y, and the solution curves are y = Ceˣ.

How are slope fields used in calculus?

In calculus, slope fields help you understand differential equations visually. In AP Calculus, typical tasks include sketching a few segments by hand, matching a slope field to its equation, and drawing the particular solution through a given point. They also reveal equilibrium solutions, which appear as horizontal rows of flat segments where dy/dx = 0 for every x.

How can slope fields be explained simply?

Think of a weather map with tiny arrows showing which way the wind blows at each spot. A slope field does the same for a differential equation: each small segment shows which way a solution would head if it passed through that point. Drop a pencil at a starting point, follow the segments, and you have sketched a solution curve.

Related Lessons You May Like

• How to find the slope of a line
• How to find the equation of a line
• How to find the derivative of a function
• How to solve systems of equations
• How to find volume by spinning: disk method

For a friendly introduction to slope fields and differential equations, Calculus for Beginners walks through slope fields, separable equations, and basic integration. Pre-Calculus for Beginners covers the algebra and trig prerequisites.