Unlocking the Secrets of Curves: Higher Order Derivatives in Graph Analysis

When we take the derivative of a function, we start with that function; if the function is complex enough, the derivative will also gonna be a function, and not a constant number or zero (even though they are technically functions too), which can then be further derived into another function, and so on. if we take further derivatives of a derivative of a function, we are taking the higher order derivatives. for example, take \( x^3 \) function, here are the derivative of this function and the higher order derivatives:

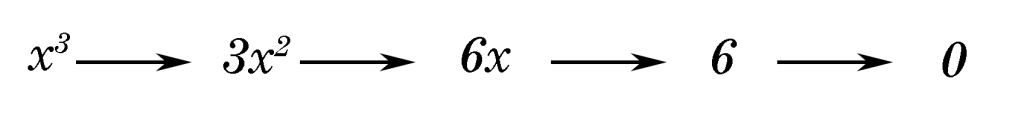
After a certain number of derivatives, we reach zero, which normally suggests no further differentiation is necessary. However, in mathematical theory, differentiation can continue indefinitely. This concept, while yielding zeros in subsequent derivatives for polynomial functions like \( f(x) = x^3 \), is fundamental in advanced mathematics. It forms the basis for understanding properties like smoothness and is crucial in Taylor series expansions, where functions are expressed in terms of their derivatives. In practical applications, especially in physics and engineering, knowing a function is infinitely differentiable helps in modeling and analyzing complex dynamic systems, even if higher-order derivatives are zero.

Let’s consider this radical function: \( f(x) = \sqrt{3x + 5} \). We’ll find the first few derivatives of this function.

1. First Derivative: To find the first derivative of \( f(x) = \sqrt{3x + 5} \), we use the chain rule, as we have a composition of functions (the square root function and the linear function \( 3x + 5 )\):
   \( f'(x) = \frac{1}{2\sqrt{3x + 5}} \cdot 3 = \frac{3}{2\sqrt{3x + 5}} \)
2. Second Derivative: Differentiating the first derivative, we get:
   \( f”(x) = \frac{d}{dx}\left( \frac{3}{2\sqrt{3x + 5}} \right) = -\frac{9}{4}(3x + 5)^{-\frac{3}{2}} \)
   This derivative involves applying the quotient rule or further application of the chain rule.
3. Subsequent Derivatives: here are the next derivatives:

3rd: \( \frac{81}{8\left(3x+5\right)^{\frac{5}{2}}} \)

4th: \( \frac{-1215}{16\left(3x+5\right)^{\frac{7}{2}}} \)

5th: \( \frac{25515}{32\left(3x+5\right)^{\frac{9}{2}}} \)

and so on, which can go on forever.

here are the graphs for these functions, starting from the original function, \( f(x) = \sqrt{3x + 5} \), with each graph representing the “graph of changes” of the previous function at every \( x \) value: