How to Finding Range, Quartile and Interquartile Range

The interquartile range is the middle half of the data.
To discover IQR, follow these steps:
Step 1: Find the median of the lower and upper half of the data.
These values are quartile 1 (Q_1) and quartile 3 (Q_3).
Step 2: Subtract the first quartile from the third quartile.
So, the difference between Q_3 and Q_1 is IQR.

Range: The range is a measure of how spread out the data is and is calculated as the difference between the largest and smallest values in a data set. To find the range, simply subtract the smallest value from the largest value. For example, if a data set contains the values 10, 12, 15, 17, and 20, the range would be 20-10 = 10.

Quartiles: Quartiles divide a data set into four equal parts, with each part representing 25% of the data. To find the quartiles, you need to first sort the data from smallest to largest. The first quartile (Q1) represents the 25th percentile and is the value below which 25% of the data falls. The second quartile (Q2) is the median of the data set and represents the 50th percentile. The third quartile (Q3) represents the 75th percentile and is the value below which 75% of the data falls.

Interquartile Range (IQR): The interquartile range (IQR) is a measure of how spread out the data is between the first and third quartiles. It is calculated as the difference between Q3 and Q1. To find the IQR, first calculate Q1 and Q3, and then subtract Q1 from Q3. The IQR provides a measure of variability that is more robust to outliers than the range.

A step-by-step guide finding range, quartile, and interquartile range

Here’s a step-by-step guide to finding range, quartile, and interquartile range:

1. Start by collecting and organizing the data you want to analyze. This could be a set of numbers or values from a larger data set.
2. Calculate the range by subtracting the smallest value from the largest value. This will give you an idea of how spread out the data is.
3. Sort the data from smallest to largest. This will make it easier to find the quartiles.
4. Calculate the median of the data set. This is the value that divides the data set into two equal parts. This is the second quartile (Q2).
5. Find the first quartile (Q1) by taking the median of the lower half of the data set. To do this, find the middle value of the lower half of the data set. If there are an odd number of values, include the median value in both halves.
6. Find the third quartile (Q3) by taking the median of the upper half of the data set. To do this, find the middle value of the upper half of the data set. If there are an odd number of values, include the median value in both halves.
7. Calculate the interquartile range (IQR) by subtracting Q1 from Q3. This gives you an idea of how spread out the data is between the first and third quartiles.
8. Use the range, quartiles, and IQR to draw conclusions and make comparisons between different data sets. For example, if two data sets have similar ranges but different IQRs, it may indicate that the two sets have different levels of variability.

Finding range, quartile, and interquartile range can help you analyze and draw meaningful conclusions from a data set.

By following these steps, you can understand the distribution and variability of your data and make informed decisions based on the information.

Finding Range, Quartile, and Interquartile Range – Examples

Answer the questions based on the data set.
5, 7,12, 7, 2, 10, 9, 4, 5,2
What is the lower quartile, Q_1?
What is the upper quartile, Q_3?
What is the interquartile range?
What is the range?
Solution:
Step 1: Order the data from least to greatest. 2,2,4,5,5,7,7,9,10,12
Step 2: Divide a data set into a lower half and upper half.

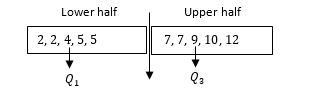
Step 3: Find the median of the lower half. So, Q_1 is 4.
Step 4: Find the median of the upper half. So, Q_3 is 9.
Step 5: Subtract the first quartile from the third quartile. \(9-4=5\). So, the interquartile range is 5.
Step 6: The greatest number is 12. The last number is 2. Subtract the least number from the greatest number. \(12-2=10\). So, the range is 10.