8th Grade MAP Math Practice Test Questions

Preparing your student for the 8th Grade MAP Math test? Help your students build MAP Math test skills by following common MAP Math questions for 8th Grade. Practicing common math questions is the best way to help your students improve their Math skills and prepare for the test. Here, we provide a step-by-step guide to solving 10 common MAP Math practice problems covering the most important math concepts on the 8th-grade MAP Math test.
The Absolute Best Book to Ace 8th Grade MAP Math Test
10 Sample 8th Grade MAP Math Practice Questions
1- Five years ago, Amy was three times as old as Mike was. If Mike is 10 years old now, how old is Amy?
A. 4
B. 8
C. 12
D. 20
2- What is the length of AB in the following figure if \(AE=4, CD=6\) and \(AC=12\)?
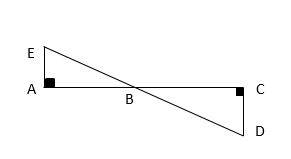
A. 3.8
B. 4.8
C. 7.2
D. 24
3- If a gas tank can hold 25 gallons, how many gallons does it contain when it is \(\frac{2}{5}\) full?
A. 50
B. 125
C. 62.5
D. 10
4- In the ??-plane, the point \((4,3)\) and \((3,2)\) are on line \(A\). Which of the following equations of lines is parallel to line \(A\)?
A. \(y=3x \)
B. \(y=\frac{x}{2}\)
C. \(y=2x \)
D. \(y=x \)
5- If \(x\) is directly proportional to the square of \(y\), and \(y=2\) when \(x=12\), then when \(x=75 y=\) ?
A. \(\frac{1}{5}\)
B. 1
C. 5
D. 12
6- Jack earns $616 for his first 44 hours of work in a week and is then paid 1.5 times his regular hourly rate for any additional hours. This week, Jack needs $826 to pay his rent, bills, and other expenses. How many hours must he work to make enough money this week?
A. 40
B. 48
C. 53
D. 54
7-
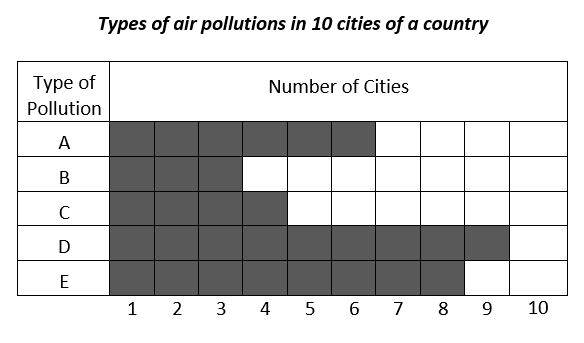
If a is the mean (average) of the number of cities in each pollution type category, b is the mode, and c is the median of the number of cities in each pollution type category, then which of the following must be true?
A. \(a<b<c\)
B. \(b<a<c\)
C. \(a=c\)
D. \(b<c=a\)
8-
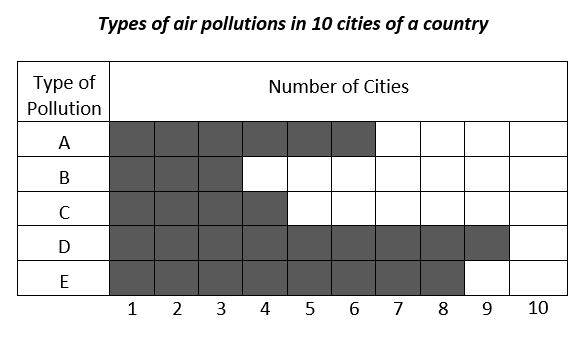
What percent of cities are in the type of pollution \(A, C,\) and \(D\) respectively?
A. \(60\%, 40\%, 90\%\)
B. \(30\%, 40\%, 90\%\)
C. \(30\%, 40\%, 60\%\)
D. \(40\%, 60\%, 90\%\)
9-
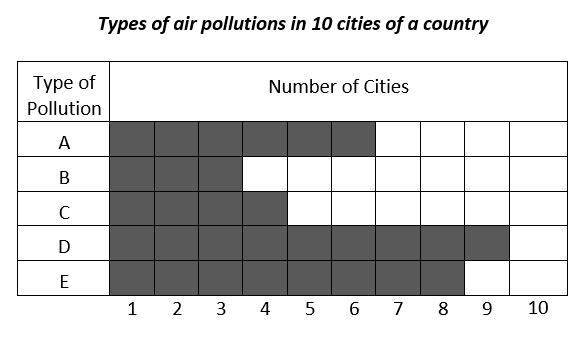
How many cities should be added to the type of pollution \(B\) until the ratio of cities in the type of pollution \(B\) to cities in the type of pollution \(E\) is 0.625?
A. 2
B. 3
C. 4
D. 5
10- In the following right triangle, if the sides \(AB\) and \(AC\) become twice longer, what will be the ratio of the perimeter of the triangle to its area?
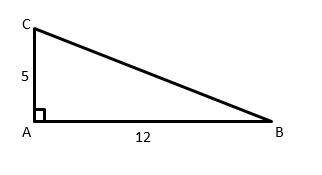
A. \(\frac{1}{2}\)
B. 2
C. \(\frac{1}{3}\)
D. 3
Best 8th Grade MAP Math Prep Resource for 2024
Answers:
1- D
Five years ago, Amy was three times as old as Mike. Mike is 10 years now. Therefore, 5 years ago Mike was 5 years.
Five years ago, Amy was: \( A=3×5=15 \)
Now Amy is 20 years old: \(15 + 5 = 20\)
2- B
Two triangles \(∆BAE\) and \(∆BCD\) are similar. Then:
\(\frac{AE}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{x}{12}\)
\(→48-4x=6x→10x=48→x=4.8\)
3- D
\(\frac{2}{5}×25=\frac{50}{5}=10\)
4- D
The slope of line A is:
\(m = \frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{4-3}=1\)
Parallel lines have the same slope and only choice \(D (y=x)\) has a slope of 1.
5- C
\(x\) is directly proportional to the square of \(y\). Then:
\(x=cy^2\)
\(12=c(2)^2→12=4c→c=\frac{12}{4}=3\)
The relationship between \(x\) and \(y\) is:
\(x=3y^2\)
\(x=75\)
\(75=3y^2→y^2=\frac{75}{3}=25→y=5\)
6- D
The amount of money that Jack earns for one hour: \(\frac{$616}{44}=$14\)
The number of additional hours that he works to make enough money is: \(\frac{$826-$616}{1.5×$14}=10\)
The number of total hours is: \(44+10=54\)
7- C
Let’s find the mean (average), mode, and median of the number of cities for each type of pollution.
Number of cities for each type of pollution: \(6, 3, 4, 9, 8\)
\(??????? (????) = \frac{sum \space of \space terms}{number \space of \space terms}=\frac{6+3+4+9+8}{5}=6\)
The median is the number in the middle. To find the median, first list numbers in order from smallest to largest.
\(3, 4, 6, 8, 9\)
The median of the data is 6.
Mode is the number that appears most often in a set of numbers. Therefore, there is no mode in the set of numbers.
\(Median = Mean, then, a=b\)
8- A
Percent of cities in the type of pollution A: \(\frac{6}{10} × 100=60\%\)
Percent of cities in the type of pollution C: \( \frac{4}{10} × 100 = 40\%\)
Percent of cities in the type of pollution D: \( \frac{9}{10}× 100 = 90\%\)
9- A
Let the number of cities be added to the type of pollution \(B\) be \(x\). Then:
\(\frac{x + 3}{8}=0.625→x+3=8×0.625→x+3=5→x=2\)
10- A
\(AB=12\) And \(AC=5\)
\(BC=\sqrt{(12^2+5^2 )} = \sqrt{(144+25)} = \sqrt{169}=13\)
\(Perimeter =5+12+13=30 \)
\(Area =\frac{5×12}{2}=5×6=30\)
In this case, the ratio of the perimeter of the triangle to its area is:
\(\frac{30}{30}= 1\)
If the sides \(AB\) and \(AC\) become twice longer, then:
\(AB=24\) And \(AC=10\)
\(BC=\sqrt{(24^2+10^2 )} = \sqrt{(576+100)} = \sqrt{676} = 26\)
Perimeter \(=26+24+10=60\)
\(Area =\frac{10×24}{2}=10×12=120\)
In this case, the ratio of the perimeter of the triangle to its area is:
\(\frac{60}{120}=\frac{1}{2}\)
Looking for the best resource to help you succeed on the 8th-grade MAP Math test?
The Best Books to Ace 8th Grade MAP Math Test
Related to This Article
More math articles
- How to Grasp Parallel Vectors
- 4th Grade Ohio’s State Tests Math Worksheets: FREE & Printable
- The Ultimate 6th Grade AzMERIT Math Course (+FREE Worksheets)
- How to Graph Linear Inequalities? (+FREE Worksheet!)
- The Ultimate ISTEP Algebra 1 Course (+FREE Worksheets)
- 4th Grade RICAS Math Worksheets: FREE & Printable
- How to Write a Formula for a Recursive Sequence
- Understanding Trigonometry: How to Calculate the Area of Triangles
- 6th Grade Georgia Milestones Assessment System Math FREE Sample Practice Questions
- How to Prepare for the FSA Math Test?












What people say about "8th Grade MAP Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.