How to Graph Absolute Value Inequalities?
To graph an absolute value inequality, first, you need to solve the absolute value inequality.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{{url}}/?ajax-add-to-cart={{id}}" product-item-button-custom-url-if-not-salable="{{productUrl}} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
The absolute value of a number describes its distance from zero. To graph absolute value inequality you must first solve the inequality and then represent absolute value inequalities on a number line.
Related Topics
A step-by-step guide to graph absolute value inequalities
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
- Find two values.
- Draw a number line and Place dots or open dots on the two points corresponding to the solutions. if the symbol is (\(≥\) or \(≤\)) then you fill in the dot if the symbol is (\(>\) or \(<\)) then you do not fill in the dot.
- Sketch a line and show all numbers the variable can be.
Graphing Absolute Value Inequalities – Example 1:
Solve and graph \(|3x-3|<9\).
Solution:
Use absolute properties: if \(|a|<b\), \(b > 0\) then: \( -b<a<b → -9 < 3x-3 < 9\)
Add \(3\) to each side of inequality: \(-9+3 < 3x-3+3 < 9+3 → -6 < 3x < 12\)
Divide each side of inequality by \(3\): \( -2 < x < 4\)
Graph it on a number line.
Graphing Absolute Value Inequalities – Example 2:
Solve and graph \(|x+2| ≥ 3\).
Solution:
Split into two inequalities: \(x+2 ≥ 3\) or \(x+2 ≤ -3\).
Subtract \(2\) from each side of each inequality:
\(x+2-2 ≥ 3-2\) → \(x ≥ 1\)
or
\(x+2-2 ≤ -3-2\) → \(x ≤ -5\)
\(x ≥ 1\) or \(x ≤ -5\).
Graph the numbers that satisfy both conditions:
Exercises for Graph Absolute Value Inequalities
Solve and graph the following inequalities.
- \(\color{blue}{4|x| ≥ 12}\)
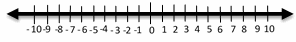
- \(\color{blue}{|x-2| < 1}\)
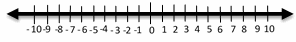
- \(\color{blue}{|x+2| ≥ 2}\)
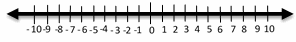
- \(\color{blue}{5|x+2| ≥ 15}\)
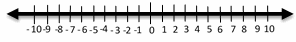
Related to This Article
More math articles
- How to Add and Subtract Matrices? (+FREE Worksheet!)
- Top Calculators for the SAT 2026: Quick Review
- Geometry Puzzle – Challenge 71
- How to Find Average Rate of Change of a Function?
- How to Solve One-Step Inequalities? (+FREE Worksheet!)
- 3rd Grade SOL Math Worksheets: FREE & Printable
- Overview of the ACCUPLACER Math Test
- A Comprehensive Collection of Free ParaPro Math Practice Tests
- Real-Life Math Problem With Credit Card Utilization
- 4th Grade NHSAS Math Worksheets: FREE & Printable
What people say about "How to Graph Absolute Value Inequalities? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.