How to Find Domain and Range of Radical Functions? (+FREE Worksheet!)
There are several different methods to identify the Domain and Range of Radical Functions. In this blog post, you will learn how to find the Domain and Range of Radical Functions.
Related Topics
- How to Add and Subtract Radical Expressions
- How to Multiply Radical Expressions
- How to Rationalize Radical Expressions
- How to Solve Radical Equations
- How to Simplify Radical Expressions
Rules for Finding Domain and Range of Radical Functions
- To find the domain of the function, find all possible values of the variable inside radical.
- Remember that having a negative number under the square root symbol is not possible. (For cubic roots, we can have negative numbers)
- To find the range, plugin the minimum and maximum values of the variable inside the radical.
Examples
Domain and Range of Radical Functions – Example 1:
Find the domain and range of the radical function. \(y=\sqrt{x-3}\)
Solution:
For domain: Find non-negative values for radicals: \(x-3≥0\)
Domain of functions: \(\sqrt{f(x)} →f(x)≥0\), Then solve \(x-3≥0→x-3+3 ≥0+3 → x≥3\)
Domain of the function \( y=\sqrt{x-3}: x≥3\)
For range: The range of a radical function of the form \(c\sqrt{ax+b}+k\) is:
\(f(x)≥k\)
For the function \(y=\sqrt{x-3}\), the value of \(k\) is \(0\). Then Range of the function \(y=\sqrt{x-3}: f(x)≥0\)
Domain and Range of Radical Functions – Example 2:
Find the domain and range of the radical function. \(y=\sqrt{x-8}+5\)
Solution:
For domain: Find non-negative values for radicals: \(x-8≥0\)
Domain of functions: \(\sqrt{f(x)} →f(x)≥0\), Then solve for \(x: x-8≥0→x-8+8 ≥ 0+8→ x≥8\)
Domain of the function \(y=\sqrt{x-8}+5:\) \(x≥8\)
For range: the range of a radical function of the form \(c\sqrt{ax+b}+k\) is \(f(x)≥k\)
For the function \(y=\sqrt{x-8}+5\), the value of \(k\) is \(5\). Then Range of the function \(y=\sqrt{x-8}+5 : f (x) ≥5\)
The Absolute Best Book for the Algebra I
Domain and Range of Radical Functions – Example 3:
Find the domain and range of the radical function. \(y=\sqrt{2x+4}+9\)
Solution:
For domain: Find non-negative values for radicals: \(2x+4≥0\)
Domain of functions: \(\sqrt{f(x)} →f(x)≥0\), Then solve for \(x: 2x+4≥0→x≥-2\)
Domain of the function \(y=\sqrt{2x+4}+9:\) \(x≥-2\)
For range: the range of a radical function of the form \(c\sqrt{ax+b}+k\) is \(f(x)≥k\)
For the function \(y=\sqrt{2x+4}+9\), the value of \(k\) is \(9\). Then Range of the function \(y=\sqrt{2x+4}+9 :\) \(f(x)≥9\)
Domain and Range of Radical Functions – Example 4:
Find the domain and range of the radical function. \(y=3\sqrt{2x-10}+6\)
Solution:
For domain: Find non-negative values for radicals: \(2x-10≥0\)
Domain of functions: \(\sqrt{f(x)} →f(x)≥0\), Then solve for \(x: 2x-10≥0→x≥5\)
Domain of the function \(y=3\sqrt{2x-10}+6:\) \(x≥5\)
For range: the range of a radical function of the form \(c\sqrt{ax+b}+k\) is \(f(x)≥k\)
For the function \(y=3\sqrt{2x-10}+6\), the value of \(k\) is \(6\). Then Range of the function \(y=3\sqrt{2x-10}+6:\) \(f(x)≥6\)
Exercises for Domain and Range Radical Functions
Identify the Domain and Range
- \(\color{blue}{y=\sqrt{x-1}}\)
- \(\color{blue}{y=2\sqrt{x+3}}\)
- \(\color{blue}{y=\sqrt{x-5}}\)
- \(\color{blue}{y=\sqrt{x+4}+2}\)
Sketch the graph of the function
5. \(\color{blue}{y=\sqrt{x}-2}\)
6. \(\color{blue}{y=3\sqrt{x}-1}\)
- \(\color{blue}{x≥1,f(x)≥0}\)
- \(\color{blue}{x≥-3,f(x)≥0}\)
- \(\color{blue}{x≥5,f(x)≥0}\)
- \(\color{blue}{x≥-4,f(x)≥2}\)
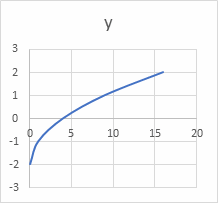
5. \(\color{blue}{y=\sqrt{x}-2}\)
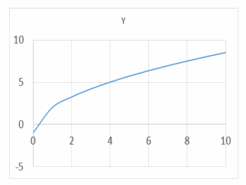
6. \(\color{blue}{y=3\sqrt{x}-1}\)
The Absolute Best Book for the Algebra Test
Related to This Article
More math articles
- How to Translate Phrases into an Algebraic Statement? (+FREE Worksheet!)
- Math Topics You Need to Learn in Medicine
- The 5 BEST Online Math Tutoring Tools
- Missing Numerals
- 4th Grade NHSAS Math Worksheets: FREE & Printable
- Benchmark Brilliance: How to Estimate Decimal Sums and Differences with Ease
- 3rd Grade WVGSA Math Worksheets: FREE & Printable
- PSAT 8/9, PSAT 10, and PSAT/NMSQT Preview
- Top 5 Best Math YouTube Channels for High School Students
- How to Divide Mixed Numbers? (+FREE Worksheet!)
What people say about "How to Find Domain and Range of Radical Functions? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.