Frequency Charts: How to Understanding Trends

A step-by-step guide to interpreting frequency charts

Frequency charts, also known as frequency distributions, are used to display the distribution of a dataset.

They provide a visual representation of the number of times each value or range of values appears in a dataset.

A frequency chart is a table expressing the frequencies of the values of the variables in a data set.

To create a frequency distribution table, you must count the frequencies.

The frequency distribution table is made to illustrate how many times the value happens.

Here is a step-by-step guide on how to interpret frequency charts:

Step 1: Determine the type of data Before interpreting a frequency chart, it’s essential to understand the type of data being represented. Data can be classified as either categorical or numerical. Categorical data consists of non-numeric values such as gender or occupation, while numerical data is made up of numeric values such as age, height, or weight.

Step 2: Identify the x-axis and y-axis The x-axis is typically the horizontal axis of a frequency chart, and it represents the different values or categories in the dataset. The y-axis, which is the vertical axis, represents the frequency or count of the occurrence of each value or category.

Step 3: Look at the shape of the distribution The shape of the distribution tells you about the distribution of the data. There are three main types of distribution: symmetrical, skewed left, and skewed right. A symmetrical distribution has values that are evenly distributed on either side of the mean. A skewed left distribution has a longer tail on the left side of the chart, while a skewed right distribution has a longer tail on the right side of the chart.

Step 4: Identify the measures of central tendency The measures of central tendency, such as the mean, median, and mode, are important measures that describe the center of the distribution. The mean is the sum of all the values divided by the total number of values, while the median is the value that falls in the middle of the distribution. The mode is the most common value in the distribution.

Step 5: Identify the measures of spread The measures of spread, such as the range, interquartile range (IQR), and standard deviation, describe how spread out the values in the distribution are. The range is the difference between the maximum and minimum values in the dataset. The IQR is the range of the middle 50% of the data, while the standard deviation is a measure of how much the values deviate from the mean.

Step 6: Draw conclusions After identifying the measures of central tendency and measures of spread, you can draw conclusions about the dataset. For example, if the distribution is skewed left, the mean may be less than the median, indicating that there are some low outliers in the dataset. Alternatively, a symmetrical distribution may have a mean and median that are similar, indicating that there are no significant outliers.

Frequency Charts – Examples 1

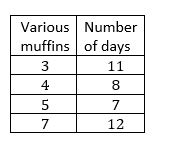
Draw the frequency chart with the help of this data.
Meg bakes various muffins for a café, every day. The following data is about the various muffins baked daily.
5,3, 3, 7, 5, 4, 7,3, 4, 7, 3, 7, 3, 3, 7, 4, 3, 5, 4,7, 4, 5, 3, 7,3, 5, 4, 3, 7, 3, 7, 7, 7, 4, 5,7,5,4.

Solution:

Count the frequencies of each muffin and write in a table.

Frequency Charts – Examples 2

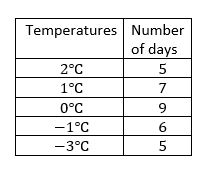
Draw the frequency chart with the help of this data.
The following data is about the daily low temperatures.
0℃,-1℃,1℃,-3℃,0℃,2℃,0℃,-1℃,-3℃,2℃,1℃,2℃,0℃,-1℃,-1℃ ,0℃,
-3℃,0℃,1℃,-3℃,1℃,1℃,2℃,0℃,-1℃,0℃,2℃,-1℃,1℃,-3℃,0℃,1℃.

Solution:

count the frequencies of each temperature and write them in the table.