How to Determine a Function Using the Vertical Line Test?
Vertical line testing helps determine whether the given equation represents a function. In this guide, you can learn about determining a function using the vertical line test.

The vertical line intersects the graph of a function at only one point and it has only one \(y\) value (codomain) for the \(x\) value (domain).
A step-by-step guide to determining a function using the vertical line test
Vertical line testing helps to determine whether a graph is a function or not. A vertical line in a coordinate system represents a set of infinite points with the same \(x\)-coordinate values and different \(y\)-coordinate values for each of its points.
The vertical line is drawn parallel to the \(y\)-axis, if it cuts the curve at one distinct point then it has one \(y\)-value for the given \(x\) value and it follows the basic definition of a function.
Vertical line testing is useful to know whether a relation is a function. The vertical line test satisfies the definition of a function: for every domain \(x\) value, there is only one range \(y\) value for the function.
The vertical line \(x = a\), if it cuts the curve \(y = f(x)\) at only one point \((a, f(a))\), then such a curve \(y=f(x)\) represents a function.
A vertical line is supposed to intersect the curve at only one point, for the curve to represent a function. And if the vertical line \(x = a\) is cutting the graph \(y = f(x)\) at more than one point, ie… at two points such as \((x, y_1 ), (x, y_2)\), then it is having different \(y\) values for the same \(x\)-value.
Thus each domain has more than one codomain value and contradicts the original definition of a function and the curve \(y = f(x)\) does not represent a function.
Graph of vertical line test
The diagram of a vertical line helps to easily determine whether the given equation \(y= f (x)\) represents a function.
In each diagram, we can quickly observe whether the vertical line intersects the curve at one point or more. If the line intersects the curve more than once, the graph does not show a function. For a function, the vertical line needs to cut the curve at only one point.
How to apply the vertical line test?
The following steps must be followed to perform the vertical line test to see if the given expression is a function. There are two ways to apply the vertical line test. It can be used geometrically or algebraically. Let’s consider a function \(y = f(x)\) and the vertical line having the equation \(x = a\).
- Geometrically:
Draw the graph of \(y=f(x)\), with respect to the coordinate axis. Now draw the line \(x=a\) and see the number of places that intersect the curve \(y= f(x)\). If this vertical line intersects the curve in more than one place, the curve does not represent a function. If the vertical line cuts the curve at only one point which is \((a, f(a))\), then the curve \(y=f(x)\) represents a function.
- Algebraically:
The equation of a vertical line is \(x=a\) and substituting it in the equation of a curve \(y = f(x)\), we get \(y = f(a)\). If we get more than one value for \(y\), it proves that the equation \(y = f (x)\) does not represent a function. In addition, if we obtain only a single value for (y\), on substituting \(x = a\) in \(y = f(x)\), then \(y = f(x)\) represents a function.
Determining a Function Using the Vertical Line Test – Example 1:
Use the vertical line test to determine whether the following graph represents a function.
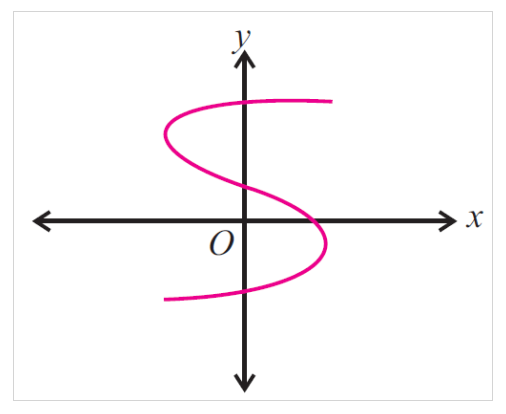
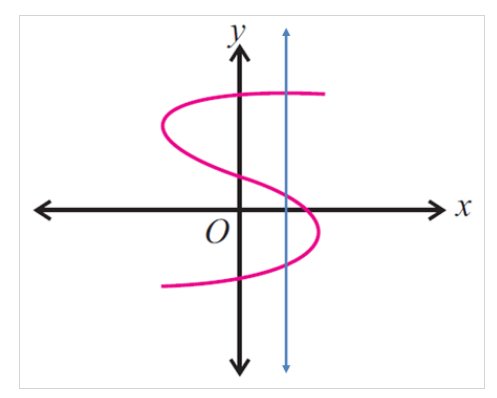
Solution:
First, draw a vertical line at any point on the given graph. And now, check whether the vertical line drawn on the diagram intersects the diagram at a maximum of one point.
The vertical line intersects the graph at more than one point (three points), then the given graph does not show a function.
Exercises for Determining a Function Using the Vertical Line Test
Use the vertical line test to determine if the following graph shows a function.
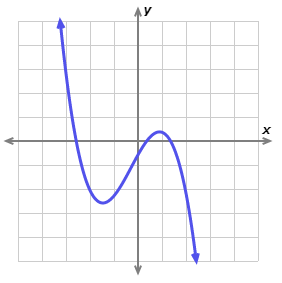
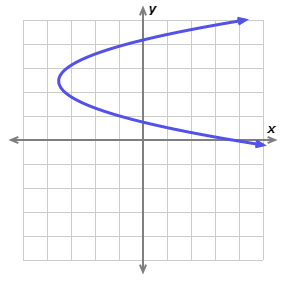

- \(\color{blue}{Yes}\)
- \(\color{blue}{No}\)
Related to This Article
More math articles
- Best Graphing Calculators for Precalculus
- 10 Most Common 7th Grade IAR Math Questions
- Reversing Derivatives Made Easy: Power Rule of Integration
- Polynomial Identity
- Dividing Dollars: How to Navigate Money Division in Word Problems
- How to Use Parallelogram Rule for Vector Addition and Subtraction
- Best Digital Writing Pads for Online Teaching in 2024
- 10 Most Common ParaPro Math Questions
- How to Use Models to Decompose Fractions into Unit Fractions?
- How to Construct Triangles? (+FREE Worksheet!)





























What people say about "How to Determine a Function Using the Vertical Line Test? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.