How to Graph Exponential Functions?

In mathematics, an exponential function is a function of form \(f(x)=a^x\), Where \(x\) is a variable and \(a\) is a constant called the base of the function and must be greater than \(0\).

Related Topics

• How to Solve Exponential Equations

A step-by-step guide to an exponential function graph

We can understand the process of graphing exponential functions with examples. Let us graph two functions \(f(x)=2^x\) and \(g(x)=(\frac{1}{2})^2\).

To plot \(f(x)=2^x\) function, we create a table of values with random values \(x\), plot the points on the chart, connect them by a curve, and extend the curve on both sides.

Here is the table of values that are used to graph the exponential function \(f(x)=2^x\).

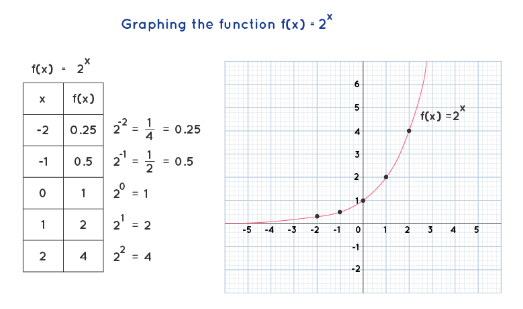
Note: the graph of exponential function \(f(x)=b^x\):

• increases when \(b > 1\)
• decreases when \(0 < b < 1\)

Domain and Range of Exponential Function

The domain of a function \(y = f (x)\) is the set of all values of \(x\) (inputs) that can be calculated, and the range is the set of all \(y\)-values (outputs) of the function.

The domain of an exponential function is the set of all real numbers (or) \((-∞, ∞)\).

The range of an exponential function can be determined by the horizontal asymptote of the graph, for example, \(y = d\), and by seeing whether the graph is above \(y = d\) or below \(y = d\).

Therefore, for an exponential function \(f(x) = ab^x\),

• The domain is the set of all real numbers (or) \((-∞, ∞)\).
• Range is \(f(x) > d\) if \(a > 0\) and \(f(x) < d\) if \(a < 0\).

Exercises for Exponential Function Graph

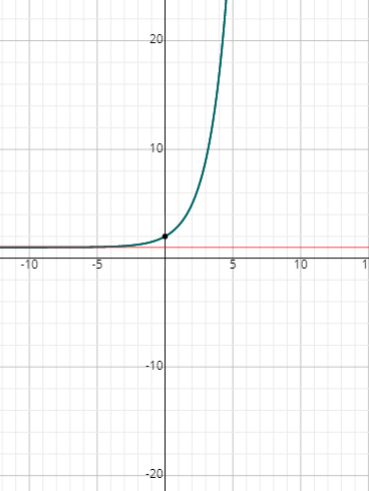
Plot the following exponential functions.

• \(\color{blue}{y=2^x+1}\)

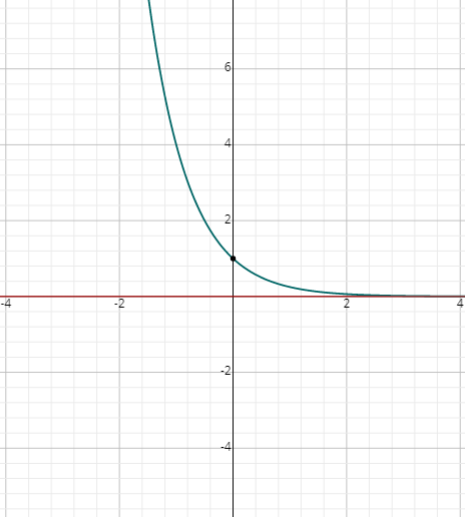
• \(\color{blue}{y=4^{-x}}\)

• \(\color{blue}{y=2^x+1}\)

• \(\color{blue}{y=4^{-x}}\)