GED Math FREE Sample Practice Questions

Preparing for the GED Math test? To do your best on the GED Math test, you need to review and practice real GED Math questions. There’s nothing like working on GED Math sample questions to hone your math skills and put you more at ease when taking the GED Math test. The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your GED Math test.
Check out our sample GED Math practice questions to find out what areas you need to practice more before taking the GED Math test!
Start preparing for the 2022 GED Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the GED Math Test
10 Sample GED Math Practice Questions
1- What is the area of a square whose diagonal is 8?
A. 16
B. 32
C. 36
D. 64
2- The perimeter of the trapezoid below is 36 cm. What is its area?
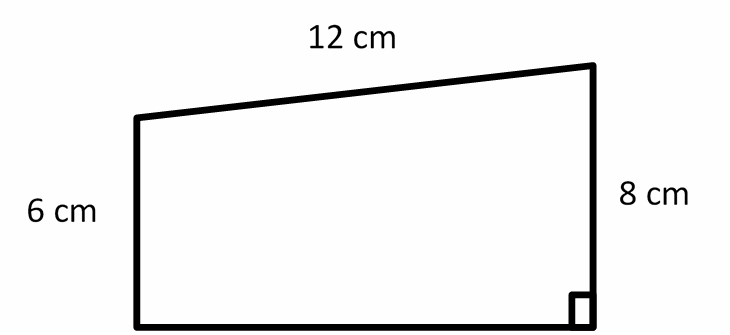
A. 576 cm\(^2\)
B. 70 cm\(^2\)
C. 48 cm\(^2\)
D. 24 cm\(^2\)
3- A bank is offering \(3.5\%\) simple interest on a savings account. If you deposit $12,000, how much interest will you earn in two years?
A. $420
B. $840
C. $4200
D. $8400
4- Which of the following graphs represents the compound inequality \(-2{\leq}2x-4<8 \)?
A.

B.

C.

D.

5- Last week 24,000 fans attended a football match. This week three times as many bought tickets, but one-sixth of them canceled their tickets. How many are attending this week?
A. 48,000
B. 54,000
C. 60,000
D. 72,000
6- The square of a number is \(\frac{25}{64} \). What is the cube of that number?
A. \(\frac{5}{8} \)
B. \(\frac{25}{254}\)
C. \(\frac{125}{512}\)
D. \(\frac{125}{64}\)
7- In the \(xy\)-plane, the point (4,3) and (3,2) are on line A. Which of the following points could also be online A?
A. \((-1, 2)\)
B. \((5, 7)\)
C. \((3, 4)\)
D. \((-1, -2)\)
8- What is the missing term in the given sequence? ____________
2, 3, 5, 8, 12, 17, 23, _, 38
9- What is the equivalent temperature of \(104^{\circ}\) F in Celsius?
C \(= \frac{5}{9} \) (F \(- 32\))
A. 32
B. 40
C. 48
D. 52
10- If \(150\%\) of a number is 75, then what is the \(90\%\) of that number?
A. 45
B. 50
C. 70
D. 85
Best GED Math Prep Resource for 2022
Answers:
1- B
The diagonal of the square is 8. Let \(x\) be the side.
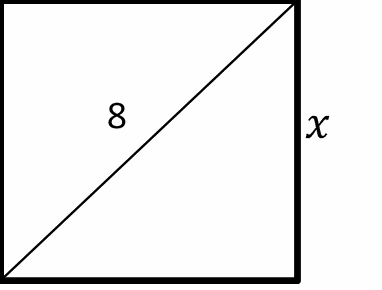
Use Pythagorean Theorem: \(a^2 + b^2 = c^2 \)
\(x^2 + x^2 = 8^2 {\Rightarrow} 2x^2 = 82 {\Rightarrow} 2x^2 = 64 {\Rightarrow}x^2 = 32 {\Rightarrow}x= {\sqrt{32}}\)
The area of the square is:
\({\sqrt{32}} {\times} {\sqrt{32}} = 32\)
2- B
The perimeter of the trapezoid is \(36 cm\).
Therefore, the missing side (height) is \(= 36 – 8 – 12 – 6 = 10\)
Area of a trapezoid: A \(= \frac{1}{2} h ({b_{1} + b_{2}}) = \frac{1}{2} (10) (6 + 8) = 70\)
3- B
Use simple interest formula:
\(I=prt\)
(I = interest, p = principal, r = rate, t = time)
\(I=(12000)(0.035)(2)=840$\)
4- D
Solve for \(x\).
\(-2 {\leq} 2x-4 < 8 ⇒\) (add 4 all sides) \(-2+4 {\leq} 2x-4+4 < 8+4 {\Rightarrow}\)
\(2{\leq}2x<12 {\Rightarrow}\) (divide all sides by 2) 1 \({\leq}x < 6\)
\(x\) is between 1 and 6.
5- C
Three times 24,000 is 72,000. One-sixth of them canceled their tickets.
One sixth of 72,000 equals \(12,000 (\frac{1}{6}) (\times ) 72000 = 12000\).
\(60,000 (72000 – 12000 = 60000)\) fans are attending this week
6- C
The square of a number is \(\frac{25}{64}\), then the number is the square root of \(\frac{25}{64}\)
\(\sqrt{\frac{25}{64}}=\frac{5}{8}\)
The cube of the number is:
\(({\frac{5}{8}})^3 = \frac{125}{512}\)
7- D
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and b is the \(y\)-intercept of the line.
Two points (4,3) and (3,2) are on line A. Therefore, the slope of the line A is:
slope of line A\(=\frac{(y_2- y_1)}{(x_2 – x_1 ) } =\frac{2-3}{3-4} = \frac{-1}{-1} \)
The slope of line A is 1. Thus, the formula of line A is:
\(y=mx+b=x+b\), choose a point and plug in the values of \(x\) and \(y\) in the equation to solve for b. Let’s choose points (4, 3). Then:
\(y=x+b \rightarrow 3=4+b\rightarrow b=3-4=-1\)
The equation of line A is: \(y=x-1\)
Now, let’s review the choices provided:
A. \((-1,2) \ \ y=x-1\rightarrow 2=-1-1=-2\) (This is not true.)
B. \((5,7) \ \ y=x-1\rightarrow 7=5-1=4\) (This is not true.)
C. \((3,4) y=x-1 \ \ \rightarrow 4=3-1=2\) (This is not true.)
D. \((-1,-2) y=x-1 \ \ \rightarrow -2=-1-1=-2\) (This is true!)
8- 30
The difference of 2 and 3 is 1, 3 and 5 is 2, 5 and 8 is 3, 8 and 12 is 4, 12 and 17 is 5, 17 and 23 is 6, 23 and next number should be 7. The number is 23 + 7 = 30
9- B
Plugin 104 for F and then solve for C.
C \(= \frac{5}{6}\) (F \(- 32) {\Rightarrow}\) C \(= \frac{5}{9} (104 – 32) {\Rightarrow} C = \frac{5}{9} (72) = 40\)
10- A
First, find the number.
Let \(x\) be the number. Write the equation and solve for \(x\).
\(150\%\) of a number is 75, then:
\(1.5{\times}x=75 {\Rightarrow} x=75{\div}1.5=50\)
\(90\%\) of 50 is:
\(0.9 {\times} 50 = 45\)
High School Equivalency Tests

The Best Books to Ace the GED Math Test
More from Effortless Math for GED Test …
Now, you have reviewed some sample GED Math questions, it’s a good idea to take a Full-Length GED Math Practice Test. You can also review our Free GED Math Practice Test.
Aiming for the best possible GED Math score?
Review our Ultimate GED Math Course to learn everything you will ever need to ace the GED Math test. Besides studying, you also need to learn about GED Math Test-Taking Strategies.
The Perfect Prep Books for the GED Math Test
Have any questions about the GED Test?
Write your questions about the GED or any other topics below and we’ll reply!
Related to This Article
More math articles
- Top 10 Tips to Overcome TABE Math Anxiety
- Best Ergonomic Chairs for Online Teachers in 2024
- 5th Grade PSSA Math FREE Sample Practice Questions
- 6th Grade MAAP Math Worksheets: FREE & Printable
- The Application of The Squeeze Theorem: Limit Problems Made Easy
- The Ultimate TABE Math Course (+FREE Worksheets & Tests)
- Number Properties Puzzle -Critical Thinking 2
- Quotient Quickies: How to Navigate Decimal Division with Estimations
- Identify 3–Dimensional Figures
- The Role of Math in Game Design



















What people say about "GED Math FREE Sample Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.