Full-Length SSAT Upper Level Practice Test-Answers and Explanations
Did you take the SSAT Upper-Level Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
SSAT Upper Level Mathematical Reasoning Practice Test Answers and Explanations
1- Choice E is correct
The area of the floor is: 9 cm \(×\) 36 cm \(=\) 324 cm\(^2\), The number of tiles needed \(= 324 ÷ 6 = 54\)
2- Choice E is correct
The number of packs is equal to \(31/4≅7.75\), Therefore, the school must purchase 7 packs.
3- Choice D is correct
\(\frac{35}{A}+2=7→\frac{35}{A}=7-2=5, →35=5A→A=\frac{35}{5}=7, 35+A=35+7=42\)
4- Choice C is correct
Number of rotates in 12 second equals to: \(\frac{400×15}{6}=1125\)
5- Choice E is correct
A. Number of books sold in April is: 610
The number of books sold in July is: 845→ \(\frac{610}{845}≅0.721\)
B. the number of books sold in July is: 845
Half the number of books sold in May is: \(\frac{1560}{2}=780→780<845 \)
C. number of books sold in June is: 210
Half the number of books sold in April is: \(\frac{610}{2}=305→210<305\)
D. \(610+210=820<845 \)
E. \(610<845\)
6- Choice D is correct
The amount of money that Jack earns for one hour: \(\frac{$756}{54}=$14\)
Several additional hours that he needs to work to make enough money is:
\(\frac{$924-$756}{1.5×$14}=8\)
The number of total hours is: \(54+8=62\)
7- Choice C is correct
The digit in tens place is 8. The digit in the thousandth place is 3. Therefore; \(8+3=11\)
8- Choice A is correct
First, find the number. Let \(x\) be the number. Write the equation and solve for \(x\).
\(160 \%\) of a number is 80, then: \(1.6×x=80→x=80÷1.6=50, 70 \%\) of 50 is: \(0.7×50=35\)
9- Choice E is correct
\(18.236÷0.004=\frac{\frac{18,236}{1,000}}{\frac{4}{1,000}}=\frac{18,236}{4}=4559\)
10- Choice E is correct
Average \(=\frac{sum of terms }{number of terms}\)
The sum of the weight of all girls is: \(12 × 55 = 660\) kg
The sum of the weight of all boys is: \(21 × 59 = 1,239\) kg
The sum of the weight of all students is: \(660 + 1,239 = 1,899\) kg
The average weight of the 50 students: \(\frac{1899}{33}=57.54\)
11- Choice D is correct
\(3≤x<6→\) Multiply all sides of the inequality by 3. Then:
\(3×3≤3×x<3×6→9≤3x<18\)
Add 5 to all sides. Then: \(→9+5≤3x+5<18+5→ 14≤3x+5<23 \)
Minimum value of \(3x+5 is 14\)
12- Choice E is correct
\(6∎13=\sqrt{6^2+13}= \sqrt{36+13}=\sqrt{49}=7\)
13- Choice C is correct
\(\frac{2 \frac{2}{3}+\frac{1}{6}}{3 \frac{3}{4}-\frac{11}{4}}=\frac{\frac{8}{3}+\frac{1}{6}}{\frac{15}{4}-\frac{11}{4}}=\frac{\frac{16+1}{6}}{\frac{15-11}{4}}=\frac{\frac{17}{6}}{\frac{4}{4}}=\frac{17×4}{6×4}=\frac{17}{6}≅2.83\)
14- Choice E is correct
Let \(x\) be the capacity of one tank. Then, \(\frac{1}{8} x=350→x=\frac{350×8}{1}=2800\) Liters
The amount of water in two tanks is equal to: \(2×2800=5600\) Liters
15- Choice E is correct
Let’s review the choices provided.
A. 4. In 4 years, David will be 62 and Ava will be 14. 62 is not 3 times 14.
B. 6. In 6 years, David will be 64 and Ava will be 16. 62 is not 3 times 16!
C. 8. In 8 years, David will be 66 and Ava will be 18. 66 is not 3 times 18.
D. 10. In 10 years, David will be 68 and Ava will be 20. 68 is not 3 times 20.
E. 14. In 14 years, David will be 72 and Ava will be 24. 72 is 3 times 24.
16- Choice B is correct
Let \(x\) be the cost of one-kilogram orange, then:
\(4x+(4×4.6)=26.4→3x+18.4=26.4→4x=26.4-18.4→4x=8→x=\frac{8}{4}=$2\)
17- Choice B is correct
All angles in a triangle sum up to 180 degrees. Then: \(x=40+105=145\)
18- Choice A is correct
\(9.5÷0.25=\frac{9.5}{0.25}=\frac{\frac{95}{10}}{\frac{25}{100}}=\frac{95×100}{25×10}=\frac{95}{25}×\frac{100}{10}=3.8×10=38\)
19- Choice D is correct
Let b be the amount of time Alec can do the job, then,
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{140}→\frac{1}{420}+\frac{1}{b}=\frac{1}{140}→\frac{1}{b}=\frac{1}{140}-\frac{1}{420}=\frac{2}{420}=\frac{1}{210}\),
Then: \(b=210\) minutes
20- Choice E is correct
Choices A,B, C and D are incorrect because \(60\%\) of each of the numbers is non-whole number.
A. \(11, 60\%\) of \(11 = 0.60×11=6.6 \)
B. \(16, 60\%\) of \(16=0.60×16=9.6 \)
C. \(19, 60\%\) of \(19=0.60×19=11.4 \)
D. \(23, 60\%\) of\( 23=0.60×23=13.8 \)
E. \(35, 60\%\) of \(35=0.60×35=21\)
The Absolute Best Book to Ace the SSAT Upper Level Math Test
21- Choice B is correct
The equation of a line in slope intercept form is: \(y=mx+b\)
Solve for \(y. 8x-4y=24 ⇒ -4y=24-8x ⇒ y=(24-8x)÷(-4) ⇒ y=2x-6\), The slope is 2. The slope of the line perpendicular to this line is:
\(m_1 × m_2 = -1 ⇒ 2 × m_2 = -1 ⇒ m_2 = -\frac{1}{2}\)
22- Choice D is correct
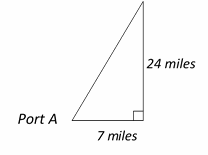
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(7^2+ 24^2 = c^2⇒\)\(49+ 576 =\)\(c^2 ⇒\)\( 625 = c^2 ⇒ c = 25\)
23- Choice D is correct
The amount of money for \(x\) bookshelf is: \(200x\)
Then, the total cost of all bookshelves is equal to: \(200x+600\)
The total cost, in dollar, per bookshelf is: \(\frac{Total cost}{number of items}=\frac{200x+600}{x}\)
24- Choice B is correct
The smallest number is \(-9\). To find the largest possible value of one of the other three integers, we need to choose the smallest possible integers for two of them. Let x be the largest number. Then: \(-40=(-9)+(-8)+(-7)+x→-40=-24+x, →x=-40+24=-16\)
25- Choice D is correct
If the length of the box is 36, then the width of the box is one third of it, 12, and the height of the box is 4 (one third of the width). The volume of the box is:
V = (length)(width)(height) = (36) (12) (4) = 1,008
26- Choice C is correct
\(\frac{87,436}{287}≅304.655≅305\)
27- Choice D is correct
Let’s review the choices provided:
A. \(x=2→\) The perimeter of the figure is: \(3+6+3+2+2=16≠30 \)
B. \( x=3→\) The perimeter of the figure is:\( 3+6+3+3+3=18≠30 \)
C. \(x=6→\) The perimeter of the figure is: \(3+6+3+6+6=24≠30 \)
D. \(x=9→\) The perimeter of the figure is: \(3+6+3+9+9=30=30 \)
E. \(x=12→\) The perimeter of the figure is: \(3+6+3+12+12=36≠30\)
28- Choice C is correct
\(\frac{14+22}{2}=\frac{36}{2}=18\) then \(18-14=4\)
29- Choice E is correct
Alex’s mark is k less than Jason’s mark. Then, from the choices provided Alex’s mark can only be \(20-k\).
30- Choice E is correct
Let’s review the options provided:
A. \(16×\frac{1}{2}=\frac{16}{2}=8=8 \)
B. \(40×\frac{1}{5}=\frac{40}{5}=8=8 \)
C. \(2×\frac{8}{2}=\frac{16}{2}=8=8 \)
D. \(6×\frac{8}{6}=\frac{48}{6}=8=8 \)
E. \(8×\frac{1}{8}=\frac{8}{8}=1≠8\)
31- Choice E is correct
Let \(x\) be the original price. If the price of the sofa is decreased by \(25\%\) to $420, then: \(50 \%\) of \(x=405 ⇒ 0.5x=405 ⇒ x=405÷0.5=810\)
32- Choice E is correct
\(860-6 \frac{8}{13}=(859-6)+(\frac{13}{13}-\frac{8}{13})=853 \frac{5}{13}\)
33- Choice E is correct
Number of times that the driver rests \(=\frac{32}{8}=4\)
Driver’s rest time = 1 hour and 5 minutes = 65 minutes
Then, \(4×65\) minutes = 260 minutes,
1 hour = 60 minutes → 260 minutes = 4 hour and 20 minutes
34- Choice A is correct
The Area that one liter of paint is required: 96cm \(×\) 100cm = 9,600cm\(^2\)
Remember: 1 m\(^2\) = 10,000 cm\(^2\) (\(100 × 100 = 10,000\)), then, 9,600cm\(^2\) = 0.96 m\(^2 \)
Number of liters of paint we need: \(\frac{48}{0.96}=50\) liters
35- Choice B is correct
Find the difference of each pair of numbers: 3, 5, 9, 17, 33, ___, 129
The difference of 3 and 5 is 2, 5 and 9 is 4, 9 and 17 is 8, 17and 33 is 16, and the next number should be 65. The number is \(33 + 32 = 65\)
36- Choice C is correct
Number of Mathematics book: \(0.3×960=288 \)
Number of English books: \(0.15×9600=144\)
Product of number of Mathematics and number of English books: \(288×144=41,472\)
37- Choice D is correct
The angle α is: \(0.3×360=108^\circ\) , The angle \(β\) is: \(0.15×360=54^\circ\)
38- Choice D is correct
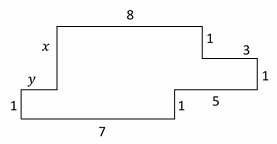
\(x+1=1+1+1→x=2 \)
\(y+8+3=7+5→y+11=12→y=1\)
Then, the perimeter is:
\(1+7+1+5+1+3+1+8+2+1=30\)
39- Choice E is correct
Let put some values for a and b. If \(a=12\) and \(b=3 →a×b=36→\frac{36}{4}=9→36\) is divisible by 4 then;
A. \(a+b=12+3=15\) is not divisible by 4
B. \(3a-b=(3×12)-3=36-3=33\) is not divisible by 4
If \(a=16\) and\( b=2 →a×b=32 →\frac{32}{4}=8\)
32 is divisible by 4 then;
C. \(a-3b=16-(3×2)=16-6=10\) is not divisible by 4
D. \(\frac{a}{3.5b}=\frac{16}{7}\) is not divisible by 4
E. \(4 ×16×2=128\)
128 is divisible by 4.
If you try any other numbers for a and b, you will get the same result.
40- Choice E is correct
The capacity of a red box is \(50\%\) bigger than the capacity of a blue box and it can hold 45 books. Therefore, we want to find a number that \(30\%\) is bigger than that number is 60. Let \(x\) be that number. Then:
\(1.50×x=45\), Divide both sides of the equation by 1. 5. Then:
\(x=\frac{45}{1.50}=30\)
Best SSAT Upper Level Math Prep Resource for 2022
41- Choice C is correct
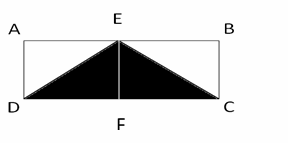
Since E is the midpoint of AB, then the area of all triangles DAE, DEF, CFE, and CBE are equal.
Let \(x\) be the area of one of the triangles than \(4x=200→x=50\)
The area of DEC \(=2x=2(50)=100\)
42- Choice D is correct
Amount of available petrol in tank: \(48.3-7.96-18.21+16.47=38.6\) liters
43- Choice E is correct
We have two equations and three unknown variables, therefore \(x\) cannot be obtained.
44- Choice A is correct
\(5y+5<51→5y<51-6→5y<45→y<9\)
The only choice that is less than 8 is E.
45- Choice C is correct
Perimeter of figure A is: \(2πr=2π \frac{14}{2}=14π=14×3=42 \)
Area of figure B is:\( 15×7=105\), Average \(=\frac{42+105}{2}=\frac{150}{2}=75\)
46- Choice C is correct
The angles on a straight line add up to 180 degrees. Let’s review the choices provided:
A. \(y=15→ x+25+y+2x+y=25+25+15+2(25)+15=130≠180\)
B. \(y=25→ x+25+y+2x+y=25+25+25+2(25)+25=150≠180 \)
C. \(y=40→ x+25+y+2x+y=25+25+40+2(25)+40=180=180 \)
D. \(y=45→ x+25+y+2x+y=25+25+45+2(25)+45=190≠180 \)
E. \(y=55→ x+25+y+2x+y=25+25+55+2(25)+55=210≠180\)
47- Choice E is correct
Let’s review the choices provided:
A. \(x=\frac{1}{2}→ \frac{2}{7}+\frac{1}{2}=\frac{4+7}{14}=\frac{11}{14}≅0.78<3 \)
B. \(x=\frac{3}{5}→ \frac{2}{7}+\frac{3}{5}=\frac{10+21}{35}=\frac{31}{35}≅0.88<3 \)
C. \(x=\frac{4}{5}→ \frac{2}{7}+\frac{4}{5}=\frac{10+28}{35}=\frac{38}{35}≅1.085<3 \)
D. \(x=\frac{4}{3}→ \frac{2}{7}+\frac{4}{3}=\frac{6+28}{21}=\frac{34}{21}≅1.61<3 \)
E. \(x=\frac{10}{3}→ \frac{2}{7}+\frac{10}{3}=\frac{6+70}{21}=\frac{76}{21}≅3.61>3 \)
Only choice E be is correct.
48- Choice B is correct
Set of numbers that are not composite between 8 and 17: A= {11, 13, 17}
Probability = \(\frac{number of desired outcomes}{number of total outcomes}=\frac{ 3}{10}\)
49- Choice C is correct
\(432÷4=\frac{432}{4}=\frac{400+30+2}{4}=\frac{400}{4}+\frac{30}{4}+\frac{2}{4}\)
50- Choice E is correct
\(\frac{4}{6}×36=\frac{144}{6}=24\)
The Best Books to Ace the SSAT Upper Level Math Test
Related to This Article
More math articles
- FREE 8th Grade MAP Math Practice Test
- Cracking the Code: How Math is Empowering Students to Solve Real-World Problems in the Digital Age
- How to Use Models to Decompose Fractions into Unit Fractions?
- Definition and Properties of Inverse Trigonometric Functions
- A Comprehensive Collection of FREE ACT Math Practice Tests
- How much Does It Cost to Retake the CBEST Test?
- How to Factor the Difference between Two Perfect Squares?
- Best Laptops for Back to School
- How to Complete a Function Table from an Equation
- The Best ALEKS Math Worksheets: FREE & Printable
What people say about "Full-Length SSAT Upper Level Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.