10 Most Common SSAT Upper-Level Math Questions

Preparing for the SSAT Upper-Level Math test? Want a preview of the most common mathematics questions on the SSAT Upper-Level Math test? If so, then you are in the right place.

The mathematics section of SSAT Upper Level can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!

Preparing for the SSAT Upper-Level Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the SSAT Upper Level can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common SSAT Upper-Level Math questions to help you know what to expect and what to practice most. Try these 10 most common SSAT Upper-Level Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.

Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the SSAT Upper-Level Math Test

10 Sample SSAT Upper-Level Math Practice Questions

1- If \(x∎y=\sqrt{x^2+y}\), what is the value of \(6∎28\)?

A. \(\sqrt{168}\)

B. 10

C. 8

D. 6

E. 4

2- If \(2≤x<6\), what is the minimum value of the following expression?

A. 9

B. 7

C. 4

D. 2

E. 1

3- What is the answer of \( 0.9÷0.015\)?

A. \(\frac{1}{60}\)

B. \(\frac{1}{6}\)

C. 6

D. 600

E. 60

4- \(\frac{1 \frac{4}{3} + \frac{1}{4}}{2 \frac{1}{2} – \frac{17}{8}}\) is approximately equal to.

A. 3.33

B. 3.6

C. 5.67

D. 6.88

E. 6.97

5- There are four equal tanks of water. If \(\frac{2}{5}\) of a tank contains 300 liters of water, what is the capacity of the four tanks of water together?

A. 1,500 liters

B. 2,000 liters

C. 2,500 liters

D. 3,000 liters

E. 3,500 liters

6- A cruise line ship left Port A and traveled 30 miles due west and then 40 miles due north. At this point, what is the shortest distance from the cruise to port A?

A. 50 miles

B. 55 miles

C. 60 miles

D. 70 miles

E. 110 miles

7- the average weight of 20 girls in a class is 55 kg and the average weight of 42 boys in the same class is 82 kg. What is the average weight of all the 62 students in that class?

A. 70 kg

B. 72.20 kg

C. 73.29 kg

D. 74.44 kg

E.75.20 kg

8- Two-kilogram apple and two-kilogram orange cost $28.4. If a one-kilogram apple costs $5.2, how much does a one-kilogram orange cost?

A. $9

B. $6.5

C. $6

D. $5.5

E. $5

9-David’s current age is 44 years, and Ava’s current age is 4 years old. In how many years David’s age will be 5 times Ava’s age?

A. 4

B. 6

C. 8

D. 10

E. 14

10- Michelle and Alec can finish a job together in 50 minutes. If Michelle can do the job by herself in 2.5 hours, how many minutes does it take Alec to finish the job?

A. 60

B. 75

C. 80

D. 100

E. 150

Best SSAT Upper-Level Math Prep Resource for 2024

Answers:

2- B
\(2≤x<6→\) Multiply all sides of the inequality by 3. Then:
\(2×3≤3×x<6×3→6≤3x<18\)
Add 1 to all sides. Then: \(→6+1≤3x+1<18+1→ 7≤3x+1<19\)
A minimum value of \(3x+1\) is 7.

3- E
\(0.90÷0.015=\frac{0.90}{0.015}=\frac{\frac{90}{100}}{\frac{15}{1,000}}=\frac{90×1,000}{15×100}=\frac{90}{15}×\frac{1,000}{100}=6×10=60\)

4- D
\(\frac{1 \frac{4}{3}+\frac{1}{4}}{2 \frac{1}{2}-\frac{17}{8}}=\frac{\frac{7}{3}+\frac{1}{4}}{\frac{5}{2}-\frac{17}{8}}=\frac{\frac{28+3}{12}}{\frac{20-17}{8}}=\frac{\frac{31}{12}}{\frac{3}{8}}=\frac{31×8}{12×3}=\frac{31×2}{3×3}=\frac{62}{9}≅6.88\)

5- D
Let \(x\) be the capacity of one tank. Then, \(\frac{2}{5 } x=300→x=\frac{300×5}{2}=750\) Liters
The amount of water in four tanks is equal to 4×750=3,000 Liters

6- A
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
\(30^2+40^2=c^2⇒900+1,600=c^2⇒2500=c^2 ⇒c=50\) miles

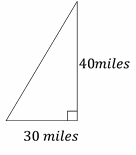
7- C
Average \(=\frac{sum \ of \ terms }{number \ of \ terms}\),
The sum of the weight of all girls is: 20×55=1,100 kg, The sum of the weight of all boys is: 42×82=3,444 kg, The sum of the weight of all students is: 1,100+3,444=4,544 kg
The average weight of the 62 students: \(\frac{4,544}{62}=73.29\) kg

8- A
Let \(x\) be the cost of one-kilogram orange, then:\( 2x+(2×5.2)=28.4→\)
\(2x+10.4=28.4→2x=28.4-10.4→2x=18→x=\frac{18}{2}=$9\)

9- B
Let’s review the choices provided.
A.4. In 4 years, David will be 48 and Ava will be 8.48 is not 5 times 8.
B.6. In 6 years, David will be 50 and Ava will be 10. 50 is 5 times 10!
C.8. In 8 years, David will be 52 and Ava will be 12.52 is not 5 times 12.
D.10. In 10 years, David will be 54 and Ava will be 14.54 is not 5 times 14.
E.14. In 14 years, David will be 58 and Ava will be 18.58 is not 5 times 18.

10- B
Let b be the amount of time Alec can do the job, (change 2.5 hours to 150 minutes) then:
\(\frac{1}{a}+\frac{1}{b}=\frac{1}{50}→\frac{1}{150}+\frac{1}{b}=\frac{1}{50}→\frac{1}{b}=\frac{1}{50}-\frac{1}{150}=\frac{2}{150}=\frac{1}{75}\) , Then: b=75 minutes

Looking for the best resource to help you succeed on the SSAT Upper-Level Math test?

The Best Books to Ace the SSAT Upper-Level Math Test