8th Grade MEAP Math Practice Test Questions

Preparing your student for the 8th Grade MEAP Math test? Help your students build MEAP Math test skills by following common MEAP Math questions for 8th Grade. Practicing common math questions is the best way to help your students improve their Math skills and prepare for the test. Here, we provide a step-by-step guide to solve 10 common MEAP Math practice problems covering the most important math concepts on the 8th Grade MEAP Math test.
The Absolute Best Book to Ace 8th Grade MEAP Math Test
10 Sample 8th Grade MEAP Math Practice Questions
1- Five years ago, Amy was three times as old as Mike was. If Mike is 10 years old now, how old is Amy?
A. 4
B. 8
C. 12
D. 20
2- What is the length of AB in the following figure if \(AE=4, CD=6\) and \(AC=12\)?
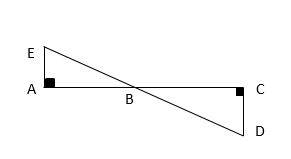
A. 3.8
B. 4.8
C. 7.2
D. 24
3- If a gas tank can hold 25 gallons, how many gallons does it contain when it is \(\frac{2}{5}\) full?
A. 50
B. 125
C. 62.5
D. 10
4- In the ??-plane, the point \((4,3)\) and \((3,2)\) are on line \(A\). Which of the following equations of lines is parallel to line \(A\)?
A. \(y=3x \)
B. \(y=\frac{x}{2}\)
C. \(y=2x \)
D. \(y=x \)
5- If \(x\) is directly proportional to the square of \(y\), and \(y=2\) when \(x=12\), then when \(x=75 y=\) ?
A. \(\frac{1}{5}\)
B. 1
C. 5
D. 12
6- Jack earns $616 for his first 44 hours of work in a week and is then paid 1.5 times his regular hourly rate for any additional hours. This week, Jack needs $826 to pay his rent, bills, and other expenses. How many hours must he work to make enough money this week?
A. 40
B. 48
C. 53
D. 54
7-
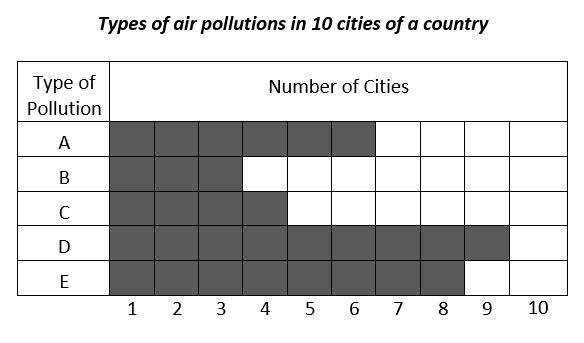
If a is the mean (average) of the number of cities in each pollution type category, b is the mode, and c is the median of the number of cities in each pollution type category, then which of the following must be true?
A. \(a<b<c\)
B. \(b<a<c\)
C. \(a=c\)
D. \(b<c=a\)
8-
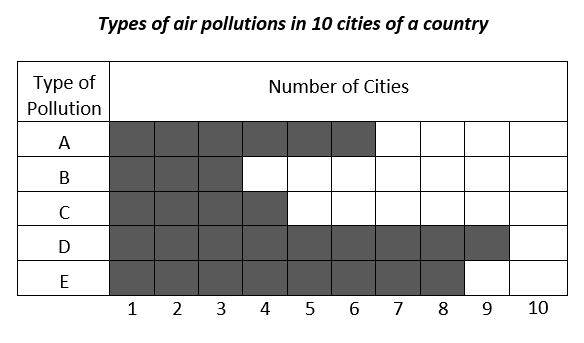
What percent of cities are in the type of pollution \(A, C,\) and \(D\) respectively?
A. \(60\%, 40\%, 90\%\)
B. \(30\%, 40\%, 90\%\)
C. \(30\%, 40\%, 60\%\)
D. \(40\%, 60\%, 90\%\)
9-
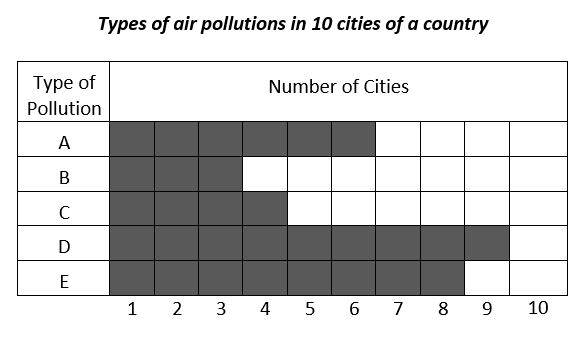
How many cities should be added to the type of pollution \(B\) until the ratio of cities in the type of pollution \(B\) to cities in the type of pollution \(E\) is 0.625?
A. 2
B. 3
C. 4
D. 5
10- In the following right triangle, if the sides \(AB\) and \(AC\) become twice longer, what will be the ratio of the perimeter of the triangle to its area?
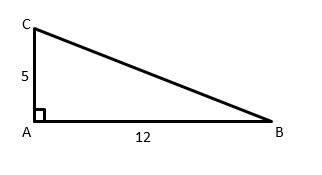
A. \(\frac{1}{2}\)
B. 2
C. \(\frac{1}{3}\)
D. 3
Best 8th Grade MEAP Math Prep Resource for 2024
Answers:
1- D
Five years ago, Amy was three times as old as Mike. Mike is 10 years old now. Therefore, 5 years ago Mike was 5 years.
Five years ago, Amy was: \( A=3×5=15 \)
Now Amy is 20 years old: \(15 + 5 = 20\)
2- B
Two triangles \(∆BAE\) and \(∆BCD\) are similar. Then:
\(\frac{AE}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{x}{12}\)
\(→48-4x=6x→10x=48→x=4.8\)
3- D
\(\frac{2}{5}×25=\frac{50}{5}=10\)
4- D
The slope of line A is:
\(m = \frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{4-3}=1\)
Parallel lines have the same slope and only choice \(D (y=x)\) has a slope of 1.
5- C
\(x\) is directly proportional to the square of \(y\). Then:
\(x=cy^2\)
\(12=c(2)^2→12=4c→c=\frac{12}{4}=3\)
The relationship between \(x\) and \(y\) is:
\(x=3y^2\)
\(x=75\)
\(75=3y^2→y^2=\frac{75}{3}=25→y=5\)
6- D
The amount of money that Jack earns for one hour: \(\frac{$616}{44}=$14\)
The number of additional hours that he works to make enough money is: \(\frac{$826-$616}{1.5×$14}=10\)
The number of total hours is: \(44+10=54\)
7- C
Let’s find the mean (average), mode, and median of the number of cities for each type of pollution.
Number of cities for each type of pollution: \(6, 3, 4, 9, 8\)
\(??????? (????) = \frac{sum \space of \space terms}{number \space of \space terms}=\frac{6+3+4+9+8}{5}=6\)
The median is the number in the middle. To find the median, first list numbers in order from smallest to largest.
\(3, 4, 6, 8, 9\)
The median of the data is 6.
Mode is the number that appears most often in a set of numbers. Therefore, there is no mode in the set of numbers.
\(Median = Mean, then, a=b\)
8- A
Percent of cities in the type of pollution A: \(\frac{6}{10} × 100=60\%\)
Percent of cities in the type of pollution C: \( \frac{4}{10} × 100 = 40\%\)
Percent of cities in the type of pollution D: \( \frac{9}{10}× 100 = 90\%\)
9- A
Let the number of cities be added to the type of pollution \(B\) be \(x\). Then:
\(\frac{x + 3}{8}=0.625→x+3=8×0.625→x+3=5→x=2\)
10- A
\(AB=12\) And \(AC=5\)
\(BC=\sqrt{(12^2+5^2 )} = \sqrt{(144+25)} = \sqrt{169}=13\)
\(Perimeter =5+12+13=30 \)
\(Area =\frac{5×12}{2}=5×6=30\)
In this case, the ratio of the perimeter of the triangle to its area is:
\(\frac{30}{30}= 1\)
If the sides \(AB\) and \(AC\) become twice longer, then:
\(AB=24\) And \(AC=10\)
\(BC=\sqrt{(24^2+10^2 )} = \sqrt{(576+100)} = \sqrt{676} = 26\)
Perimeter \(=26+24+10=60\)
\(Area =\frac{10×24}{2}=10×12=120\)
In this case, the ratio of the perimeter of the triangle to its area is:
\(\frac{60}{120}=\frac{1}{2}\)
Looking for the best resource to help you succeed on the MEAP Math test?
The Best Books to Ace MEAP Math Test
Related to This Article
More math articles
- Picture Perfect Inequalities: How to Graph Solutions of Two-Step Inequalities
- Top Proven Strategies To Increase Your SAT Math Score
- How to Solve Geometric Sequences? (+FREE Worksheet!)
- Intelligent Math Puzzle – Challenge 84
- How to Divide Polynomials Using Long Division?
- Sandy Savings: A Guide to How to Calculate Sales Tax on Your Beach Vacation
- ACT Tеѕting Accommodations fоr Studеntѕ with Diѕаbilitiеѕ
- The Challenge for The Future of Math Education
- Mastering the Lagrange Error Bound for Reliable Function Approximations
- How to Add Mixed Numbers? (+FREE Worksheet!)










What people say about "8th Grade MEAP Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.