FREE HiSET Math Practice Test

FREE HiSET Math Practice Test

Interactive HiSET Math Practice Test (Timed, 55 Questions)

Take our free, full-length HiSET Math practice test below. It mirrors the real exam: 55 multiple-choice questions in 90 minutes, calculator-neutral, covering all four HiSET Mathematics content areas. You’ll get a HiSET-style score (1–20), a breakdown of where you stand, and full step-by-step explanations after you submit. Scroll down for more HiSET math practice and study tips.

Open the full-screen timed HiSET test →

HiSET® Math Formula Sheet

Keep this handy while you practice. A formula sheet is also provided on the real HiSET® exam.

Area & Perimeter

  • RectangleArea = l × w
  • RectanglePerimeter = 2l + 2w
  • TriangleArea = ½ b h
  • ParallelogramArea = b h
  • TrapezoidArea = ½(b1 + b2)h
  • CircleArea = πr2
  • CircleCircumference = 2πr

Volume & Surface Area

  • Rectangular prismV = l w h
  • Prism (surface)SA = 2(lw + lh + wh)
  • CylinderV = πr2h
  • Cylinder (surface)SA = 2πr2 + 2πrh
  • ConeV = ⅓πr2h
  • PyramidV = ⅓ (base area) h
  • SphereV = ⁴⁄₃ πr3
  • Sphere (surface)SA = 4πr2

Algebra & Coordinate Geometry

  • Slopem = (y2 − y1) ÷ (x2 − x1)
  • Slope–intercepty = mx + b
  • Point–slopey − y1 = m(x − x1)
  • Distanced = √[(x2−x1)2 + (y2−y1)2]
  • Quadratic formula ★x = (−b ± √(b2−4ac)) ÷ 2a

Right Triangles & Rates

  • Pythagorean theorem ★a2 + b2 = c2
  • Distance–rate–time ★d = r × t
  • Simple interestI = p r t

Statistics & Probability

  • Meansum of values ÷ number of values
  • Probabilityfavorable outcomes ÷ total outcomes

★ Not printed on the official HiSET formula sheet — memorize these three.

TL;DR: Want a clean honest preview of the HiSET Math exam? This free practice test mirrors the real thing: 50 questions in 90 minutes, with the on-screen TI-30XS calculator on computer-based HiSET (or your own approved calculator on paper-based). Time yourself the way test day will run, then use the answer key to grade your work. You will walk away knowing your pacing and exactly which topics still need a little more drilling.

Key takeaways:

  • HiSET Math has 50 questions and a 90-minute time limit.
  • Computer-based HiSET provides an on-screen TI-30XS scientific calculator.
  • Paper-based testers must bring their own approved scientific calculator.
  • Passing the math subtest requires a score of 8 or higher on a 1-20 scale.
  • A formula reference page is provided on every administration of the test.

The Absolute Best Book to Ace the HiSET Math Test

HiSET Math for Beginners 2026: The Ultimate Step by Step Guide to Preparing for the HiSET Math Test

HiSET Math for Beginners 2026 The Ultimate Step by Step Guide to Preparing for the HiSET Math Test

Original price was: $27.99.Current price is: $17.99.
Satisfied 184 Students

10 Sample HiSET Math Practice Questions

1- Solve for \(x\):
\(4(x + 1) = 6(x − 4) + 20\)

A. 12

B. 8

C. 6.2

D. 5.5

E. 4

2- What is \(2.5\%\) of 1,200?

A. 900

B. 600

C. 300

D. 60

E. 30

3- \((2x + 2y)(5x + 2y) =?\)

A. \(2x^2+ 14xy + 2y^2\)

B. \(2x^2+ 4xy + 2y^2\)

C. \(7x^2+ 14xy + y^2\)

D. \(10x^2+ 14xy + 2y\)

E. \(10x^2 + 14xy + 4y^2\)

4- Which of the following expressions is equivalent to
\(2x (4 + 2y)\)?

A. \(6xy + 8x\)

B. \(8xy + 8x\)

C. \(xy + 8\)

D. \(2xy + 8x\)

E. \(4xy + 8x\)

5- If \(y = 4ab + 3b³\), what is\( y\) when \(a = 2\) and \(b = 3\)?

A. 24

B. 31

C. 36

D. 51

E. 105

6- 11 yards 6 feet and 4 inches equals to how many inches?

A. 388

B. 468

C. 472

D. 476

E. 486

7- 5 less than twice a positive integer is 83. What is the integer?

A. 39

B. 41

C. 42

D. 44

E. 50

8- A shirt costing $200 is discounted \(15\%\). After a month, the shirt is discounted another \(15\%\). Which of the following expressions can be used to find the selling price of the shirt?

A. \((200) (0.70)\)

B. \((200) – 200 (0.30)\)

C. \((200) (0.15) – (200) (0.15)\)

D. \((200) (0.85) (0.85)\)

E. \((200) (0.85) (0.85) – (200) (0.15)\)

9- Which of the following points lies on the line \(2x + 4y = 10\)

A. \((2, 1)\)

B. \((–1, 3)\)

C. \((–2, 2)\)

D. \((2, 2)\)

E. \((2, 8)\)

10- \(5 + 8 × (–2) – [4 + 22 ×5] ÷ 6 =\)?

A. 120

B. 88

C. \(-45\)

D. \(-40\)

E. \(-30\)

11- The price of a car was $20,000 in 2014, $16,000 in 2015 and $12,800 in 2016. What is the rate of depreciation of the price of car per year?

A. \(15 \%\)

B. \(20 \%\)

C. \(25 \%\)

D. \(30 \%\)

E. \(30 \%\)

12- The width of a box is one third of its length. The height of the box is one third of its width. If the length of the box is 27 cm, what is the volume of the box?

A. \(81 cm^3\)

B. \(162 cm^3\)

C. \(243 cm^3\)

D. \(729 cm^3\)

E. \(1880 cm^3\)

13- If \(60 \%\) of A is \(20 \%\) of B, then B is what percent of A?

A. \(3 \%\)

B. \(30 \%\)

C. \(200 \%\)

D. \(300 \%\)

E. \(900 \%\)

14- How many possible outfit combinations come from six shirts, three slacks, and five ties?

A. 11

B. 14

C. 15

D. 30

E. 90

15- A ladder leans against a wall forming a 60\(^\circ\)angle between the ground and the ladder. If the bottom of the ladder is 30 feet away from the wall, how long is the ladder?

A. 30 feet

B. 40 feet

C. 50 feet

D. 60 feet

E. 120 feet

16- If \(f(x)= 2x^3+5x^2+2x\) and\( g(x) = -2\), what is the value of \(f(g(x))\)?

A. 36

B. 32

C. 24

D. 4

E. 0

17- The diagonal of a rectangle is 10 inches long and the height of the rectangle is 8 inches. What is the perimeter of the rectangle?

A. 10 inches

B. 12 inches

C. 16 inches

D. 18 inches

E. 28 inches

18- The perimeter of the trapezoid below is 36 cm. What is its area?

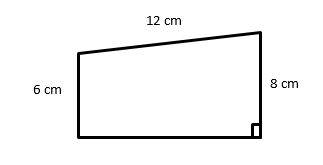
A. \(48 cm^2\)

B. \(70 cm^2\)

C. \(140 cm^2\)

D. \(576 cm^2\)

E. \(986 cm^2\)

19- A card is drawn at random from a standard 52–card deck, what is the probability that the card is of Hearts? (The deck includes 13 of each suit clubs, diamonds, hearts, and spades)

A. \(\frac{1}{3}\)

B. \(\frac{1}{4}\)

C. \(\frac{1}{6}\)

D. \(\frac{1}{52}\)

E. \(\frac{1}{104}\)

20- Which of the following shows the numbers in descending order?
\(\frac{2}{3}, 0.68, 67\%,\frac{4}{5} \)

A. \(67\%, 0.68, 2/3, 4/5\)

B. \(67\%, 0.68, 4/5, 2/3\)

C. \(0.68, 67\%, 2/3, 4/5\)

D. \(2/3, 67\%, 0.68, 4/5\)

E. \(2/3, 67\%, 4/5, 0.68\)

Best HiSET Math Prep Resource for 2026

Answers:

1- E
Simplify:
\(4(x + 1) = 6(x − 4) + 20\)
\(4x + 4 = 6x − 24 + 20\)
\(4x + 4 = 6x – 4\)
Subtract \(4x\) from both sides:
\(4 = 2x – 4\)
Add 4 to both sides:
\(8 = 2x\)
\(4 = x\)

2- E
\(2.5\%\) of \(1,200 = 0.025 × 1200 = 30\)

3- E
Use FOIL (First, Out, In, Last)
\((2x + 2y)(5x + 2y) = 10x^2+ 4xy + 10xy + 2y^2 = 10x^2+ 14xy + 4y^2\)

4- E
Use distributive property:
\(2x (4 + 2y) = 8x + 4xy = 4xy+ 8x\)

5- E
\(y = 4ab + 3b³\)
Plug in the values of a and b in the equation: \(a = 2 \)and \(b = 3\)
\(y = 4 (2) (3) + 3 (3)3 = 24 + 3(27) = 24 + 81 = 105\)

6- C
\(11 × 36 + 6 × 12 + 4 = 472\)

7- D
Let \(x\) be the integer. Then:
\(2x – 5 = 83\)
Add 5 both sides: \(2x = 88\)
Divide both sides by \(2: x = 44\)

8- D
To find the discount, multiply the number by \((100\% – rate of discount)\).
Therefore, for the first discount we get: \((200) (100\% – 15\%) = (200) (0.85) = 170\)
For the next \(15 \%\) discount: \((200) (0.85) (0.85)\)

9- B
Plug in each pair of number in the equation:
A. \((2, 1): 2 (2) + 4 (1) = 8\)
B. \((–1, 3): 2 (–1) + 4 (3) = 10\)
C. \((–2, 2): 2 (–2) + 4 (2) = 4\)
D. \((2, 2): 2 (2) + 4 (2) = 12\)

10- E
Use PEMDAS (order of operation):
\(5 + 8 × (–2) – [4 + 22 ×5] ÷ 6 = 5 + 8 × (–2) – [4 + 110] ÷ 6 = 5 + 8 × (–2) – [114] ÷ 6 = 5 + (–16) – 19 = 5 + (–16) – 19 = –11 – 19 = –30\)

11- B
Use this formula: Percent of Change
\(\frac{New \space Value-Old \space Value}{Old \space Value}× 100 \%\)
\(\frac{16000-20000}{20000}× 100 \% = 20 \%\)
and
\(\frac{12800-16000}{16000}× 100 \% = 20 \%\)

12- D
If the length of the box is 27, then the width of the box is one third of it, 9, and the height of the box is 3 (one third of the width). The volume of the box is:
\(V = lwh = (27) (9) (3) = 729\)

13- D
Write the equation and solve for B:
\(0.60 A = 0.20 B\), divide both sides by 0.20, then you will have \(0.60/0.20 A = B\), therefore:
\(B = 3\) A, and B is 3 times of A or it’s \(300\%\) of A.

14- E
To find the number of possible outfit combinations, multiply number of options for each factor:
\(6 × 3 × 5 = 90\)

15- D
The relationship among all sides of special right triangle
30\(^\circ\)-60\(^\circ\)- 90\(^\circ\) is provided in this triangle:

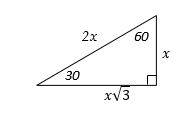
In this triangle, the opposite side of 30\(^\circ\) angle is half of the hypotenuse.
Draw the shape of this question:
The latter is the hypotenuse. Therefore, the latter is 60 ft

16- E
\(g(x)=-2, then f(g(x))= f(-2)=2 (-2)^3+5(-2)^2+2(-2)= -16+20-4=0\)

The Best Quick Study Guide for the HiSET Math Test

17- E
Let \(x\) be the width of the rectangle. Use Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(x^2 + 8^2 = 10^2 ⇒ x^2 + 64 = 100 ⇒ x^2 = 100 – 64 = 36 ⇒ x = 6\)
Perimeter of the rectangle \(= 2 (length + width) = 2 (8 + 6) = 2 (14) = 28\)

18- B
The perimeter of the trapezoid is 36.
Therefore, the missing side (height) is \(= 36 – 8 – 12 – 6 = 10\)
Area of a trapezoid: \(A = \frac{1}{2}h (b_{1} + b_{2}) = \frac{1}{2} (10) (6 + 8) = 70\)

19- B
The probability of choosing a Hearts is \(13/52 = 1/4\)

20- D
Change the numbers to decimal and then compare.
\(\frac{2}{3}= 0.666…\)
0.68
\(67% = 0.67\)
\(\frac{4}{5} = 0.80\)

High School Equivalency Tests

Looking for the best resource to help you succeed on the HiSET Math test?

The Best Books to Ace the HiSET Math Test

HiSET Math Study Guide: Step-By-Step Guide to Preparing for the HiSET Math Test

HiSET Math Study Guide Step-By-Step Guide to Preparing for the HiSET Math Test

Original price was: $20.99.Current price is: $16.99.
Satisfied 49 Students

Recommended EffortlessMath Books

If you want a complete prep workbook to study alongside this practice test, the HiSET Math for Beginners walks through every topic with worked examples. For full prep with multiple practice tests, see the HiSET Math Test Prep Bundle.

Frequently Asked Questions

How many questions are on the HiSET Math test?

50 multiple-choice questions. The content split is roughly 19% numbers and operations, 28% algebra, 18% geometry, and 35% data analysis/statistics/probability. Time limit is 90 minutes.

Is a calculator allowed on HiSET Math?

Yes. On computer-based HiSET, an on-screen TI-30XS scientific calculator is available throughout the math subtest. On paper-based HiSET, you bring your own approved non-graphing scientific calculator from the official approved list.

Is there a formula sheet on the HiSET?

Yes. Every HiSET Math administration includes a formula reference page covering area, perimeter, volume, the Pythagorean theorem, simple interest, slope, and the distance formula. The quadratic formula and trig identities are NOT on the sheet.

What score do I need to pass HiSET Math?

A subtest score of 8 (on the 1-20 scale) is the typical minimum for math. You also need a total of 45 across all five subtests with no subtest below 8, plus at least 2 out of 6 on the writing essay. Some states require higher minimums.

How long is the HiSET Math test?

90 minutes for 50 questions, so about 1 minute 48 seconds per question on average. Most testers finish with a few minutes to spare. The on-screen calculator can chew up time if you’re not familiar with the TI-30XS — practice with one before test day.

Is HiSET easier than the GED?

The HiSET gives you a formula sheet and a longer time-per-question, so many adult learners find it more forgiving. The GED is shorter (115 minutes for 46 questions) but denser. Test content is roughly comparable.

Can I retake just the HiSET Math subtest?

Yes. HiSET allows you to retake individual subtests. Most states allow up to 3 attempts per subject per year. Your passing scores on other subtests carry over.

Is HiSET computer-based or paper-based?

Both. Computer-based HiSET is offered at PSI test centers and includes the on-screen TI-30XS. Paper-based HiSET is offered at many adult learning centers. Content and scoring are identical between the two formats.

How long should I study for the HiSET Math test?

Most adult learners need 6 to 12 weeks of consistent study at 30-60 minutes per day to go from rusty to ready. Start with a full-length practice test as your diagnostic, then target your weakest content area.

Where do I get HiSET Math answer explanations?

Detailed answer explanations for this practice test live on the linked Answers and Explanations page (math-topics/full-length-hiset-math-practice-test-answers-and-explanations). Each explanation walks through the step-by-step math behind every correct choice.

Related EffortlessMath Lessons

If a topic on this practice test feels rusty, these short lessons go deeper:

Effortless Math Team

Effortless Math Team

Related to This Article

HiSET Math HiSET Math Test HiSET Score HiSET Test

More math articles

What people say about "FREE HiSET Math Practice Test - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply

X
44% OFF

Limited time only!

Save Over 44%

Take It Now!

SAVE $28

It was $64.99 now it is $36.99

The Most Comprehensive HiSET Math Preparation Bundle: Includes HiSET Math Prep Books, Workbooks, and Practice Tests
Dallas, Texas
info@EffortlessMath.com

Free math practice in your inbox

Worksheets, practice tests, and study tips for your exam. No spam.

Since 2014Helping students master math
7,000+Worksheets, books & resources
1,000,000+Satisfied students
100+ examsStandardized, state & certification
Free Resources
Popular Test Prep
Math Books
Company & Trust

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

Effortless Math: We Help Students Learn to LOVE Mathematics - © 2026