How to Find the Center and the Radius of Circles? (+FREE Worksheet!)
To find the center and radius of a circle from its equation, you need to find the equation of the circle in is the center-radius form.
Related Topics
- How to Find Arc Length and Sector Area
- How to Find Equation of a Circle
- How to Find the Area and Circumference of Circles
Rules for Finding the Center and the Radius of Circles
To find the center and the radius of a circle using the equation of the circle:
- Write the equation of the circle in standard form: \((x- h)^2+( y-k)^2= r^2\),
- The center of the circle is at \(h,k\), and its radius is \(r\).
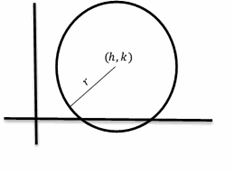
Find the Center and the Radius of Circles – Example 1:
Identify the center and the radius of each circle.
\(x^2+ y^2-4x+3=0\)
Solution:
\((x- h)^2+( y-k)^2= r^2\) is the circle equation with a radius \(r\), centered at \(h,k\).
Rewrite \(x^2+ y^2-4x+3=0\) in the standard form:
\(x^2+ y^2-4x+3=0→(x-2)^2+(y-0)^2=1^2 \)
Then, the center is at: \((2,0)\) and \(r=1\)
The Absolute Best Book for the Algebra I
Find the Center and the Radius of Circles – Example 2:
Identify the center and the radius of each circle.
\(8x+x^2+10y=8- y^2\)
Solution:
\((x- h)^2+( y-k)^2= r^2\) is the circle equation with a radius \(r\), centered at \(h,k\).
Rewrite the equation in standard form:
\(8x+x^2+10y=8- y^2→(x-(-4))^2+(y-(-5))^2=7^2 \)
Then, the center is at \((-4,-5)\) and the \(r=7\).
Find the Center and the Radius of Circles – Example 3:
Identify the center and radius.
\(8x+x^2-2y=8- y^2 \)
Solution:
\((x- h)^2+( y-k)^2= r^2\) is the circle equation with a radius \(r\), centered at \(h,k\).
Rewrite \(8x+x^2-2y=8- y^2\) in the standard form:
\((x-(-4))^2+(y-1)^2=5^2\)
Then, the center is at \((-4,1)\) and \(r=5\)
The Absolute Best Book for the Algebra Test
Related to This Article
More math articles
- 3rd Grade STAAR Math Practice Test Questions
- The Ultimate CHSPE Math Course (+FREE Worksheets & Tests)
- Top 10 3rd Grade Common Core Math Practice Questions
- Top 10 Free Websites for CHSPE Math Preparation
- How to Find the Domain and Range of Quadratic Functions
- Best Calculators fоr Algеbrа
- Touchscreen Monitors for Online Teaching
- 3rd Grade PACE Math Worksheets: FREE & Printable
- Best Office Chairs for Online Math Teachers
- Best Calculators for High School Algebra I
What people say about "How to Find the Center and the Radius of Circles? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.