Top 10 8th Grade STAAR Math Practice Questions

Preparing students for the 8th Grade STAAR Math test? The best way to prepare your students for the STAAR Math test is to work through as many STAAR Math practice questions as possible. Here are the top 10 8th Grade STAAR Math practice questions to help your students review the most important 8th Grade Math concepts. These 8th Grade STAAR Math practice questions are designed to cover mathematics concepts and topics that are found on the actual test. The questions have been fully updated to reflect the latest 2022 8th Grade STAAR guidelines. Answers and full explanations are provided at the end of the post.
Help your students start their STAAR Math test prep journey right now with these sample STAAR Math questions.
The Absolute Best Book to Ace 8th Grade STAAR Math Test
8th Grade STAAR Math Practice Questions
1- A rope weighs 600 grams per meter in length. What is the weight in kilograms of 12.2 meters of this rope? (1 kilograms = 1000 grams)
A. 0.0732
B. 0.732
C. 7.32
D. 7320
2- In a school, the ratio of the number of boys to girls is 3:7. If the number of boys is 180, what is the total number of students in the school?__________
Write your answer in the box below.
3- In two successive years, the population of a town is increased by \(15\%\) and \(20\%\). What percent of its population is increased after two years?
A. 32
B. 35
C. 38
D. 68
4- Which graph shows a non–proportional linear relationship between \(x\) and \(y\)?
A.
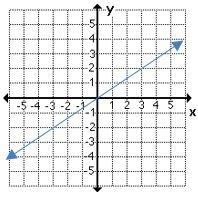
B.
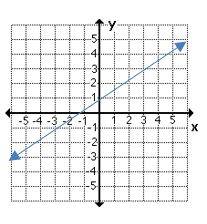
C.
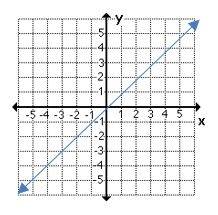
D.
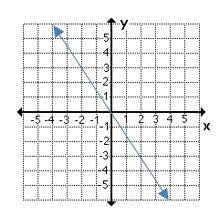
5- In the rectangle below if \(y>5\) cm and the area of a rectangle is 50 cm\(^2\) and the perimeter of the rectangle is 30 cm, what is the value of x and y respectively?

A. \(4, 11\)
B. \(5, 11\)
C. \(5, 10\)
D. \(4, 10\)
6- A football team had $40,000 to spend on supplies. The team spent $22,000 on new balls. New sports shoes cost $240 each. Which of the following inequalities represent how many new shoes the team can purchase.
A. \(240x+22,000 ≤40,000 \)
B. \(240x+22,000 ≥40,000\)
C. \(22,000x+240 ≤40,000\)
D. \(22,000x+240 ≥40,000\)
7- Right triangle ABC has two legs of lengths 6 cm (AB) and 8 cm (AC). What is the length of the third side (BC)?
A. 4 cm
B. 6 cm
C. 8 cm
D. 10 cm
8- If \(3x-5=8.5\), What is the value of \(5x+3\)?
A. 13
B. 15.5
C. 20.5
D. 25.5
9- A bank is offering \(4.5\%\) simple interest on a savings account. If you deposit $8,000, how much interest will you earn in five years?
A. $360
B. $720
C. $1800
D. $3600
10- In a party, 10 soft drinks are required for every 12 guests. If there are 252 guests, how many soft drinks is required?
A. 21
B. 105
C. 210
D. 2510
Best 8th Grade STAAR Math Prep Resource for 2022
Answers:
1- C
The weight of 12.2 meters of this rope is: \(12.2 × 600 g = 7320 g\)
\(1 kg = 1000 g\)
therefore,
\(7320 g ÷ 1000 = 7.32 kg\)
2- 600
The ratio of boys to girls is \(3:7\).
Therefore, there are 3 boys out of 10 students. To find the answer, first, divide the number of boys by 3, then multiply the result by 10.
\(180 ÷ 3 = 60 ⇒ 60 × 10 = 600\)
3- C
the population is increased by \(15\%\) and \(20\%\). \(15\%\) increase changes the population to \(115\%\) of the original population.
For the second increase, multiply the result by \(120\%\).
\((1.15) × (1.20) = 1.38 = 138\%\)
38 percent of the population is increased after two years.
4- B
A linear equation is a relationship between two variables, \(x\) and \(y\), that can be put in the form \(y = mx + b\).
A non-proportional linear relationship takes on the form \(y=mx + b\), where \(b ≠ 0\) and its graph is a line that does not cross through the origin.
5- C
The perimeter of the rectangle is: \(2x+2y=30→x+y=15→x=15-y \)
The area of the rectangle is: \(x×y=50→(15-y)(y)=50→y^2-15y+50=0\)
Solve the quadratic equation by factoring method.
\((y-5)(y-10)=0→y=5 \)
(Unacceptable, because y must be greater than 5) or \(y=10\)
If \( y=10 →x×y=50→x×10=50→x=5\)
6- A
Let \(x\) be the number of new shoes the team can purchase. Therefore, the team can purchase \(240 x\).
The team had $40,000 and spent $22,000. Now the team can spend on new shoes $18,000 at most.
Now, write the inequality: \( 120x+22.000 ≤40.000\)
7- D
Use Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(6^2 + 8^2 = c^2 ⇒ 100 = c^2 ⇒ c = 10\)
8- D
\(3x-5=8.5→3x=8.5 + 5=13.5→x = \frac{13.5}{3}= 4.5\)
Then;
\(5x+3=5 (4.5)+3=22.5+3=25.5\)
9- C
Use simple interest formula:
\(I=prt\)
\((I = interest, p = principal, r = rate, t = time)\)
\(I=(8000)(0.045)(5)=1800\)
10- C
Let \(x\) be the number of soft drinks for 252 guests. Write the proportion and solve for \(x\).
\(\frac{10 soft drinks}{12 guests}=\frac{x}{252 guests}\)
\(x = \frac{252×10}{12}⇒x=210\)
Looking for the best resource to help you succeed on the 8th Grade STAAR Math test?
The Best Books to Ace 8th Grade STAAR Math Test
Related to This Article
More math articles
- A Comprehensive Look at Average vs Instantaneous Rate of Change
- What Level of Math is Tested on the PSAT/NMSQT?
- Other Topics Puzzle – Challenge 94
- TExES Core Subjects Math- Test Day Tips
- Full-Length 8th Grade SBAC Math Practice Test
- 5th Grade TCAP Math Worksheets: FREE & Printable
- SAT Math Vs. High School Math
- How Is the CBEST Test Scored?
- What to Consider When Retaking the ACT or SAT
- The Ultimate 7th Grade North Carolina EOG Math Course (+FREE Worksheets)













What people say about "Top 10 8th Grade STAAR Math Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.