Full-Length 8th Grade SBAC Math Practice Test

Taking a Full-length 8th Grade SBAC Math practice test is the best way to help you get familiar with the test format and feel more confident. Not only will this help you measure your exam readiness and solidify the concepts you’ve learned, but it is the best way to simulate test day.
To help you get the best out of this complete and realistic 8th Grade SBAC Math practice test and prepare your mind and body for the actual test, we recommend that you treat this practice test as a real test. Prepare scratch papers, a pencil, a timer, and a calculator and take the test in one sitting and follow the time limits to the minute.
Take the following full-length 8th Grade SBAC Math practice test to simulate the test day experience. After you’ve finished, score your tests using the answer keys.
Good luck!

The Absolute Best Book to Ace the 8th Grade SBAC Math Test

Time to refine your Math skill with a practice test

Take a REAL 8th Grade SBAC Mathematics test to simulate the test day experience. After you’ve finished, score your test using the answer key.

Before You Start

• You’ll need a pencil, a calculator, and a timer to take the test.
• It’s okay to guess. You won’t lose any points if you’re wrong. So be sure to answer every question.
• After you’ve finished the test, review the answer key to see where you went wrong.
• Calculators are permitted for the 8th Grade SBAC Math Test.
• Use the answer sheet provided to record your answers.
• The 8th Grade SBAC Mathematics test contains a formula sheet, which displays formulas relating to geometric measurement and certain algebra concepts. Formulas are provided to test-takers so that they may focus on the application, rather than the memorization, of formulas.
• For each multiple-choice question, there are five possible answers. Choose which one is best.

Good Luck!

Best 8th Grade SBAC Math Prep Resource for 2022

8th Grade SBAC Math Practice Test

1- A pizza cut into 8 slices. Jason and his sister Eva ordered two pizzas. Jason ate \(\frac{1}{2}\) of his pizza and Eva ate \(\frac{3}{4}\) of her pizza. What part of the two pizzas was left?

A. \(\frac{1}{2}\)

B. \(\frac{1}{3}\)

C. \(\frac{3}{8}\)

D. \(\frac{5}{8}\)

2- Robert is preparing to run a marathon. He runs \(3 \frac{1}{10}\) miles on Saturday and two times that many on Monday and Wednesday. Robert wants to run a total of 18 miles this week. How many more miles does he need to run?

3- 20 more than twice a positive integer is 68 What is the integer?

A. 24

B. 28

C. 26

D. 30

4- \([3× (-21)+(5×2)]-(-25)+[(-3)×6]÷2=?\)

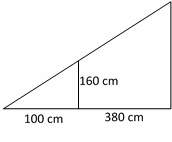
5- A girl 160 cm tall, stands 380 cm from a lamp post at night. Her shadow from the light is 100 cm long. How high is the lamp post?

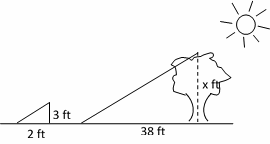
6- If a tree casts a 38 ft shadow at the same time that a yardstick casts a 2 ft shadow, what is the height of the tree?

A. 24 ft.

B. 27 ft.

C. 57 ft.

D. 48 ft.

7- Mike is 7.5 miles ahead of Julia running at 5.5 miles per hour and Julia is running at the speed of 8 miles per hour. How long does it take Julia to catch Mike?

A. 2 hours

B. 5.5 hours

C. 7.5 hours

D. 3 hours

8- A company pays its employer \($7,000\) plus \(2\%\) of all sales profit. If \(x\) is the number of all sales profit, which of the following represents the employer’s revenue?

A. \(0.02x\)

B. \(0.98x-7,000\)

C. \(0.02x+7,000\)

D.  \(0.98x+7,000\)

9- Jason needs an \(75\%\) average in his writing class to pass. On his first 4 exams, he earned scores of \(68\%\), \(72\%\), \(85\%\), and \(90\%\). What is the minimum score Jason can earn on his fifth and final test to pass?

10- If \(25\%\) of a number is 8, what is the number?

A. 30

B. 34

C. 32

D. 36

11- An angle is equal to one fifth of its supplement. What is the measure of that angle?

A. 20

B. 30

C. 45

D. 60

12- Which graph shows linear equation \(y=-2x+1\)?

A.

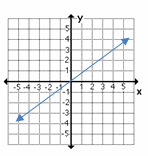
B.

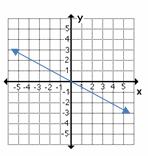
C.

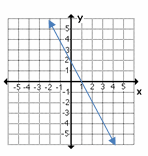
D.  

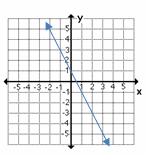
13- What is the solution of the following system of equations?
\(\begin{cases}\frac{-x}{2}+\frac{y}{4}=1\\\frac{-5y}{6}+2x=4\end{cases}\)

A. \(x=48,y=22\)

B. \(x=50,y=20\)

C. \(x=20,y=50\)

D. \(x=22,y=48\)

14- Which of the following values for \(x\) and \(y\) satisfy the following system of equations?
\(\begin{cases}x+4y=10\\5x+10y=20\end{cases}\)

A. \(x=3,y=2\)

B. \(x=2,y-3\)

C. \(x=-2,y=3\)

D. \(x=3,y=-2\)

15- The average of 21, 18, 16 and \(x\) is 20. What is the value of \(x\)?

A. 23

B. 25

C. 30

D.  20

16- Which of the equation represents the compound inequality?
\(5≤3x-1<11\)

A. \(3≤x<5\)

B. \(2≤x<4\)

C. \(2≤x<6\)

D. \(1≤x<4\)

17- Point A \((–2,6)\) and point B \((13,-2)\) are located on a coordinate grid. Which measurement is closest to the distance between point A and point B?

A. 8 units

B. 13 units

C. 15 units

D. 17 units

18- Point A \((9,7)\) and point B \((4,-5)\) are located on a coordinate grid. Which measurement is closest to the distance between point A and point B?

A. 8 units

B. 13 units

C. 15 units

D. 17 units

19- In the \(xy\)-plane, the point \((-8,8)\) and \((4,-10)\) are on line A. Which of the following equations of lines is parallel to line A?

A. \(y=\frac{3}{2} x+4\)

B. \(y=\frac{x}{2}-3\)

C. \(y=2x+4\)

D. \(y=-\frac{3}{2} x-4\)

20- What is the \(x\)-intercept of the line with equation \(10x-4y=5\)?

A. \(-5\)

B. \(-2\)

C. \(\frac{1}{2}\)

D. \(\frac{5}{4}\)

21- Giselle works as a carpenter and as a blacksmith. She earns $20 as a carpenter and $25 as a blacksmith. Last week, Giselle worked both jobs for a total of 30 hours and earned a total of $690. How long did Giselle work as a carpenter last week, and how long did she work as a blacksmith?

A. (12, 20)

B. (10, 18)

C. (12, 18)

D. (14, 16)

22- Which of the following values for x and y satisfy the following system of equations?
\(\begin{cases}3x+y=8\\-5x-2y=0\end{cases}\)

A. \(x=16,y=20\)

B. \(x=-16,y=35\)

C. \(x=12,y=40\)

D. \(x=16,y=-40\) 

23- A ride in a taxicab costs $1.25 for the first mile and $1.15 for each additional mile. Which of the following could be used to calculate the total cost \(y\) of a ride that was \(x\) miles?

A. \(x=1.25(y-1)+1.15\)

B. \(x=1.15(y-1)+1.25\)

C. \(y=1.25(x-1)+1.15\)

D. \(y=1.15(x-1)+1.25\)

24- A caterer charges $120 to cater a party for 15 people and $200 for 25 people. Assume that the cost, \(y\), is a linear function of the number of \(x\) people. Write an equation in slope-intercept form for this function. What does the slope represent? How much would a party for 40 people cost?

A. $280

B. $330

C. $300

D. $320

25- An attorney charges a fixed fee on $250 for an initial meeting and $150 per hour for all hours worked after that. Write a linear equation representation of the cost of hiring this attorney. Find the charge for 25 hours of work.

A. $4,000.00

B. $4,200.00

C. $3,800.00

D. $4,600.00

26- The sum of two numbers is 30. One of the numbers exceeds the other by 8. Find the numbers.

A. 9, 15

B. 12, 20

C. 10, 18

D. 11, 19

27- How is this number written in scientific notation?
0.0000005823

A. \(0.5823× 10^{-10}\)

B. \(5.823 × 10^{-6}\)

C. \(5.823 × 10^{-7}\)

D. \(58.23 × 10^{-5}\)

28- How is this number written in scientific notation?
28,000,000,000

A. \(2.8×10^9\)

B. \(2.8×10^{10}\)

C. \(28×10^{12}\)

D. \(2.8×10^8\)

29- Calculate the area shaded region.

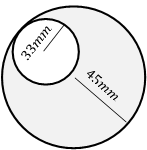
A. \(2,950 \space mm^2\)

B. \(2,940 \space mm^2\)

C. \(3,000 \space mm^2\)

D. \(2,930 \space mm^2\)

30- A circle is graphed on a coordinate grid and then reflected across the \(y\)–axis. If the center of the circle was located at \((x,y)\), which ordered pair represents the new center after the transformation?

A. \((x,y)\)

B. \((x,-y)\)

C. \((-x,y)\)

D. \((-x,- y)\)

The Best Books to Ace the 8th Grade SBAC Math Test

Answers and Explanations