How to Find the Polar Form of Complex Numbers?

Complex numbers can be represented in polar form, which is a different approach than rectangular form. Complex numbers are typically represented as \(z = x+iy\), where \((x, y)\) is the rectangular coordinates. 

Related Topics

• Identities of Complex Numbers
• How to Find Distance and Midpoint of Complex Numbers
• How to Solve the Complex Plane

Step by step guide to the polar form of complex numbers

Complex numbers are expressed in polar form as the combination of the modulus \(r\) and the complex numbers argument \(θ\). With coordinates of \((x,y)\), we can express the complex number in the manner of \(\color{blue}{z = r cos θ +i\ r sin θ= r ( cos θ + i\ sin θ )}\).

The polar form is represented with the help of polar coordinates of real and imaginary numbers in the coordinate system. Complex number \(A = x+i y\) in two-dimensional coordinate system:

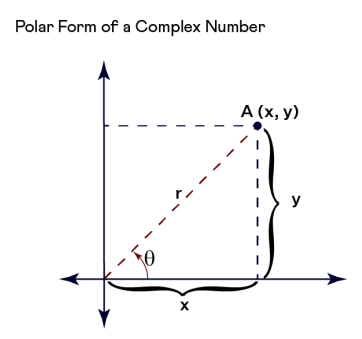
• In this image above, we have:

\(\color{blue}{cos\ θ=\frac{x}{r}}\) ⇒ \(\color{blue}{x=r cos\ θ }\)

\(\color{blue}{sin\ θ=\frac{y}{r}}\) ⇒ \(\color{blue}{y=r sin\ θ }\)

• And using Pythagoras theorem,we have:

\(\color{blue}{r^2=x^2+y^2}\) ⇒ \(\color{blue}{r=\sqrt{(x^2+y^2)}}\)

\(\color{blue}{tan\ θ=\frac{y}{x}}\) ⇒ \(\color{blue}{θ=tan^{-1}(\frac{y}{x})}\)

• For example, the horizontal and vertical axes are known as the real and imaginary axes.

• In the complex number polar form, \(r\) is the length of the vector, and \(θ\) is the angle it makes with the real axis.

• A point with coordinates \(A\) exists \((x, y)\).

• As you can see, \(r\) is the distance from \((0,0)\) to point \(A\).

• The line connecting \(A\) with origin produces a \(90\)-degree angle with a positive \(x\)-axis.

• As you can see, the polar coordinates \((r, θ)\) and the rectangle coordinates \((x, y)\) are both listed here \((x, y)\).

Complex-number polar form equation

With coordinates of \((x,y)\), we can express the complex number in the manner of \(z = r cos θ +i\ r sin θ = r ( cos θ + i\ sin θ )\). The abbreviated polar form of a complex number is \(z=r\ cis θ \), where \(r=\sqrt{(x^2+y^2)}\), and \( θ =tan^{-1}\frac{y}{x}\).

The polar form of a complex number has the following components:

• The absolute value of a complex number is represented by the symbol \(r\).

• Angle \(θ\) – The complex number argument is called the angle.

The Polar Form of Complex Numbers – Example 1:

Write the complex number in polar form. \(5+3i\)

First, find the absolute value of \(r\) by using this formula: \(\color{blue}{r=|z|=\sqrt{(x^2+y^2)}}\)

\(r=\sqrt{(5^2)+(3)^2} =\sqrt{25+9}=\sqrt{34}\)

\(r=\sqrt{34}≈5.83\)

Then, find the argument \(θ\) by using this formula: \(\color{blue}{θ=tan^{-1}(\frac{y}{x})}\).

\( θ =tan^{-1}(\frac{3}{5})=arctan(\frac{3}{5})=0.54\)

Now, write the polar form by using this formula: \(\color{blue}{z =r ( cos θ + i\ sin θ )}\).

\(z=5.83(cos(0.54)+i\sin(0.54))\)

The Polar Form of Complex Numbers – Example 2:

Write the complex number in polar form. \(3+4i\)

First, find the absolute value of \(r\) by using this formula: \(\color{blue}{r=|z|=\sqrt{(x^2+y^2)}}\)

\(r=\sqrt{(3^2)+(4)^2} =\sqrt{9+16}=\sqrt{25}\)

\(r=\sqrt{25} = 5\)

Then, find the argument \(θ\) by using this formula: \(\color{blue}{θ=tan^{-1}(\frac{y}{x})}\).

\( θ =tan^{-1}(\frac{4}{3})=arctan(\frac{4}{3})=0.92\).

Now, write the polar form by using this formula: \(\color{blue}{z =r ( cos θ + i\ sin θ )}\).

\(z=5(cos(0.92)+i\sin(0.92))\)

Exercises for the Polar Form of Complex Numbers

Write the complex number in the polar form.

1. \(\color{blue}{5i}\)
2. \(\color{blue}{-3+3i}\)
3. \(\color{blue}{2+i}\)
4. \(\color{blue}{3+7i}\)

1. \(\color {blue}{z=5(cos(\frac{π}{2})+i sin(\frac{π}{2}))}\)
2. \(\color {blue}{z=3\sqrt{2}(cos(\frac{-π}{4})+i sin(\frac{-π}{4}))}\)
3. \(\color {blue}{z=\sqrt{5}(cos(0.46)+i sin(0.46))}\)
4. \(\color {blue}{z=\sqrt{58}(cos(1.16)+i sin(1.16))}\)