How to Find Modulus (Absolute Value) and Argument (Angle) of Complex Numbers?

One of the most important things about numbers, whether they are real or complex, is that they have an “absolute value”. Keep in mind that if a real number is positive or negative, its absolute value \(|x|\) is itself.

If \(x\) is negative, its absolute value \(|x|\) is its negation, which is the positive value of \(x\). Because \(|3|\) is \(3\) and \(| –4|\) is \(4\). Removes the sign from a real number.

Related Topics

• Identities of Complex Numbers
• How to Solve the Complex Plane

A step-by-step guide to modulus and argument of complex numbers

In the complex plane \(C\), the distance from \(z\) to \(0\) is called the absolute value \(|z|\). This will make it easier to understand what absolute value is for real numbers.

The absolute value \(|x|\) of a real number \(x\) can be thought of as the distance from \(x\) to \(0\) on the real number line, so this will make it easier to understand what absolute value is.

Using the Pythagorean theorem, we can figure out how far we are from \(|z|\). Think about a right-angled triangle with one point at \(0\) and two points on each side of it. The third point is on the real line that is directly below or above the point at which the point is.

The horizontal side of the triangle is \(|x|\) long, the vertical side is \(|y|\) long, and the diagonal side is \(|z|\) long, so the triangle is a right triangle. Therefore:

\(\color{blue}{ |z|^2 =x^2+y^2}\)

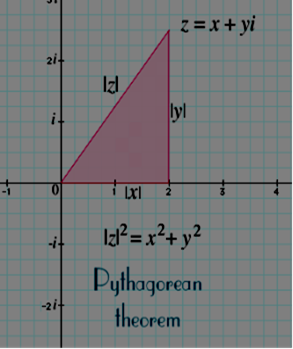
(Note that when squaring real numbers like \(x\), we can drop the absolute value because \(|x|^2 = x^2)\). This provides us a formula for \(|z|\), which is as follows:

\(\color{blue}{ |z| =\sqrt {x^2+y^2}}\)

The argument of a complex number is defined as the angle formed between the real axis and the complex number represented on the complex plane, where the real axis is the origin of the complex number. It is signified by the characters “\(θ\)” or “\(φ\)”. It is measured in radians, which is the standard unit of measurement.

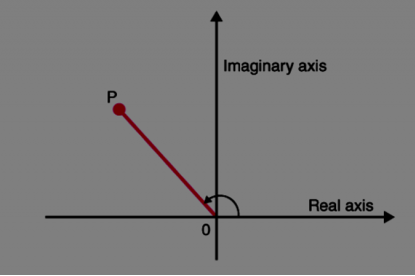
Point \(P\) denotes the complex number in this diagram. The length of the \(OP\) is known as the magnitude or modulus of a number, while the angle at which the \(OP\) is inclined from the positive real axis is the argument of the point \(P\).

The formula for complex numbers argumentation

A complex number can be expressed in polar form as \(r (cos\ θ + i sin\ θ)\), where is the \(θ \) argument. The argument function \(arg(z)\) where \(z\) denotes the complex number, \(z=(x+iy)\). The formula for calculating the complex argument is as follows:

\(\color{blue}{ arg (z) =arg (x+iy)= tan^{–1}(\frac {y}{x})}\)

Thus, the argument is expressed as follows:

\(\color{blue}{ θ =tan^{–1}(\frac {y}{x})}\)

Complex number argument properties

Now, let us look at some of the characteristics that complex numbers and their arguments share.

• If \(n\) is an integer and \(z\) is a complex number, then:

\(\color{blue}{arg\ (z^n)=n\ arg (z)}\)

• \(Z_1\) and \(Z_2\) are two complex numbers that we can suppose to have the following properties:

\(\color{blue}{ arg (\frac {z_1}{z_2})=arg (z_1)-arg(z_2)}\)

\(\color{blue}{arg\ (z_1 z_2)= arg (z_1) + arg (z_2)}\)

What is the best way to find the argument of a complex number?

1. From the given complex number, determine the real and imaginary components. \(x\) and \(y\) should be referred to as such.
2. In the formula \(\color{blue}{ θ =tan^{–1}(\frac {y}{x})}\), substitute the appropriate values.
3. If the formula returns a standard value, find the value of \(tan^{–1}\) and write it in the form of \(tan^{–1}\) itself if there is no standard value.
4. The needed value of the complex argument for the specified complex number is this value followed by the unit “radian”.

The Modulus and Argument of Complex Numbers – Example 1:

Find the argument of the complex number. \(z= 3+3\sqrt{3} i\)

In \(z=3+3\sqrt{3} i\) : the real part is \(x=3\) and imaginary part \(y= 3\sqrt{3}\).

Now, to find the argument of a complex number use this formula: \(\color{blue}{ θ =tan^{–1}(\frac {y}{x})}\).

\( θ =tan^{–1}(\frac { 3\sqrt{3} }{3})\) \(=tan^{-1}\sqrt{3}\)

\(θ\) \(=tan^{-1}\sqrt{3}=arctan \sqrt {3}=\frac{ π}{3} \)

Therefore, the argument of the complex number is \(\frac {π}{3}\) radian.

The Modulus and Argument of Complex Numbers – Example 2:

Find the modulus of a complex number. \(z=-5+3i\)

Use this formula to find the modulus of a complex number: \(\color{blue}{ |z| =\sqrt {x^2+y^2}}\)

\(|z| =\sqrt {(-5)^2+(3)^2}\)\(=\sqrt {25+9}\)\(=\sqrt {34}\)

The Modulus and Argument of Complex Numbers – Example 3:

If \(arg ({z_1})=\frac{7π }{6}\) and \(arg ({z_2})=\frac{-π }{2}\), find the \(arg ( z_1 z_2)\).

To find the \(arg ( z_1 z_2)\) use this formula: \(\color{blue}{arg\ (z_1 z_2)= arg (z_1) + arg (z_2)}\)

\(arg ( z_1 z_2)\) \(= \frac{7π }{6} + \frac{-π }{2} = \frac{7π }{6} – \frac{π }{2} =\frac{ 7π -3 π }{6}=\frac {4π}{6}=\frac{2π}{3}\)

Exercises for the Modulus and Argument of Complex Numbers

Find the modulus of a complex number.

• \(\color{blue}{ z= {2+i}}\)
• \(\color{blue}{ z= {10-6i}}\)

Find the argument of a complex number.

• \(\color{blue}{ z= {\sqrt{3}-i}}\)
• \(\color{blue}{ z= {-4-4i}}\)

• \(\color{blue}{ |z| =\sqrt {5}}\)
• \(\color{blue}{ |z| =8}\)
• \(\color{blue}{ θ=\frac{-π}{6}}\)
• \(\color{blue}{ θ=\frac{π}{4}}\)