SAT Math Practice Test Questions
Preparing for the SAT Math test? Try the following FREE SAT Math Practice Questions. Reviewing practice questions is the best way to brush up on your Math skills. Here, we walk you through solving 10 common SAT Math practice problems covering the most important math concepts on the SAT Math test.
These SAT Math practice questions are designed to be similar to those found on the real SAT Math test. They will assess your level of preparation and will give you a better idea of what to study for your exam.
The Absolute Best Book to Ace the SAT Math Test
10 Sample SAT Math Practice Questions
1- When 5 times the number \(x\) is added to 10, the result is 35. What is the result when 3 times \(x\) is added to 6?
A. 10
B. 15
C. 21
D. 25
2- What is the ratio of the minimum value to the maximum value of the following function?
\(f(x)=-3x+1\)
\(-2 ≤ x ≤ 3\)
A. \(\frac{7}{8}\)
B. \(-\frac{8}{7}\)
C. \(-\frac{7}{8}\)
D. \(\frac{8}{7}\)
3- If \(8+2x\) is 16 more than 20, what is the value of \(6x\)?
A. 40
B. 55
C. 62
D. 84
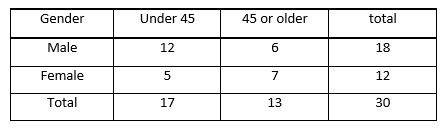
4- The table above shows the distribution of age and gender for 30 employees in a company. If one employee is selected at random, what is the probability that the employee selected to be either a female under age 45 or a male age 45 or older?
A. \(\frac{5}{6}\)
B. \(\frac{5}{30}\)
C. \(\frac{6}{30}\)
D. \(\frac{11}{30}\)
5- What is the value of \(x\) in the following system of equations?
\(5x+2y=3\)
\(y=x\)
A. \(\frac{3}{7}\)
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. \(\frac{4}{3}\)
6- If \(y=nx+2\), where n is a constant, and when \(x=6, y=14\), what is the value of y when \(x=10\)?
A. 10
B. 12
C. 18
D. 22
7- Which of the following numbers is NOT a solution to the inequality \(2x-5≥3x-1\)?
A. \(-2\)
B. \(-4\)
C. \(-5\)
D. \(-8\)
8- \(4x^2+6x-3 , 3x^2-5x+8\)
Which of the following is the sum of the two polynomials shown above?
A. \(5x^2+3x+4\)
B. \(4x^2−6x+3\)
C. \(7x^2+x+5\)
D. \(7x^2+5x+1\)
9-The table above shows some values of linear function \(g(x)\). Which of the following defines \(g(x)\)?
A. \(g(x)=2x+1\)
B. \(g(x)=2x−1\)
C. \(g(x)=−2x+1\)
D. \(g(x)=x+2\)
10- If \(\frac{6}{5}=\frac{3}{2}\), what is the value of \(y\)?
A. \(\frac{5}{6}\)
B. \(\frac{5}{4}\)
C. \(\frac{4}{5}\)
D. \(\frac{3}{2}\)
Best SAT Math Workbook Resource for 2022
Answers:
1- C
When 5 times the number \(x\) is added to 10, the result is
\(10 + 5x\). Since this result is equal to 35, the equation \(10 + 5x = 35\) is true.
Subtracting 10 from each side of \(10 + 5x = 35\) gives \(5x=25\),
and then dividing both sides by 5 gives \(x=5\).
Therefore, 3 times \(x\) added to 6, or
\(6 + 3x\), is equal to \(6 + 3(5) = 21\).
2- B
Since \(f(x)\) is linear function with a negative slop, then when \(x=-2, f(x)\) is maximum and when \(x = 3, f(x)\) is minimum. Then the ratio of the minimum value to the maximum value of the function is:
\(\frac{f(3)}{f(-2)}=\frac{-3(3)+1}{-3(-2)+1}=\frac{-8}{7}=-\frac{8}{7}\)
3- D
The description \(8+2x\) is 16 more than 20 can be written as the equation \(8+2x=16+20\), which is equivalent to \(8+2x=36\).
Subtracting 8 from each side of \(8+2x=36\) gives \(2x=28\).
Since \(6x\) is 3 times \(2x\), multiplying both sides of \(2x=28\) by 3 gives \(6x = 84\)
4- D
Of the 30 employees, there are 5 females under age 45 and 6 males age 45 or older. Therefore, the probability that the person selected will be either a female under age 45 or a male age 45 or older is: \(\frac{5}{30} + \frac{6}{30} = \frac{11}{30}\)
5- A
Substituting \(x\) for \(y\) in first equation.
\(5x+2y=3\)
\(5x+2(x)=3\)
\(7x=3\)
Divide both side of \(7x = 3\) by 3 gives \(x =\frac{3}{7}\)
6- D
Substituting 6 for \(x\) and 14 for \(y\) in \(y = nx+2\) gives \(14=(n)(6)+2\),
which gives \(n=2\). Hence, \(y=2x+2\).
Therefore, when \(x = 10\), the value of \(y\) is
\(y=(2)(10)+2 = 22\)
7- A
Subtracting \(2x\) and adding 5 to both sides of \(2x – 5 ≥ 3x – 1\) gives \(-4 ≥ x\).
Therefore, x is a solution to \(2x – 5 ≥ 3x – 1\) if and only if \(x\) is less than or equal to \(-4\) and x is NOT a solution to \(2x – 5 ≥ 3x – 1\) if and only if \(x\) is greater than \(-4\).
Of the choices given, only \(-2\) is greater than \(-4\) and, therefore, cannot be a value of \(x\).
8- C
The sum of the two polynomials is \((4x^2+6x-3)+(3x^2-5x+8)\)
This can be rewritten by combining like terms:
\((4x^2+6x-3)+(3x^2-5x+8)=(4x^2+3x^2 )+(6x-5x)+(-3+8)=
7x^2+x+5\)
9- C
Plugin the values of \(x\) in the choices provided. The points are \((1,-1)\),\((2,-3)\),and \((3,-5)\)
For \((1,-1)\) check the options provided:
A. \(g(x)=2x+1→−1=2(1)+1→−1=3A.g(x)=2x+1→−1=2(1)+1→−1=3\) This is NOT true.
B. \(g(x)=2x−1→−1=2(1)−1=1B.g(x)=2x−1→−1=2(1)−1=1\) This is NOT true.
C. \(g(x)=−2x+1→−1=2(−1)+1→−1=−1C.g(x)=−2x+1→−1=2(−1)+1→−1=−1\) This is true.
C. \(g(x)=x+2→−1=1+2→−1=3C.g(x)=x+2→−1=1+2→−1=3\) This is NOT true.
10- B
To solve the equation for \(y\), multiply both sides of the equation by the reciprocal of \(\frac{6}{5}\), which is \(\frac{5}{6}\),
this gives \(\frac{5}{6}× \frac{6}{5}y=\frac{3}{2} ×\frac{5}{6}\), which simplifies to
\(y=\frac{15}{12}=\frac{5}{4}\)
College Entrance Tests
Looking for the best resource to help you succeed on the SAT Math test?
The Best Books to Ace the SAT Math Test
Related to This Article
More math articles
- Matching a Model with a Ratio
- Unraveling More about Limits at Infinity
- 6th Grade ACT Aspire Math FREE Sample Practice Questions
- Calculus Simplified: Essential Integral Formulas for Mathematical Success
- Word Problems Involving Money
- Intelligent Math Puzzle – Challenge 90
- FREE 4th Grade PARCC Math Practice Test
- 5th Grade MAP Math Practice Test Questions
- How to Use a Graph to Factor Polynomials
- FREE 6th Grade Georgia Milestones Assessment System Math Practice Test
What people say about "SAT Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.