How to Find Reference Angles?

Related Topics

• How to Solve Coterminal Angles and Reference Angles?

Step-by-step guide to finding reference angles

The reference angle is the smallest possible angle formed by the terminal side of the given angle with the \(x\)-axis. It is always an acute angle (except when it is exactly \(90°\)). A reference angle is always positive regardless of which side the axis is falling.

To draw a reference angle for an angle, specify its end side and see at what angle the terminal side is closest to the \(x\)-axis.

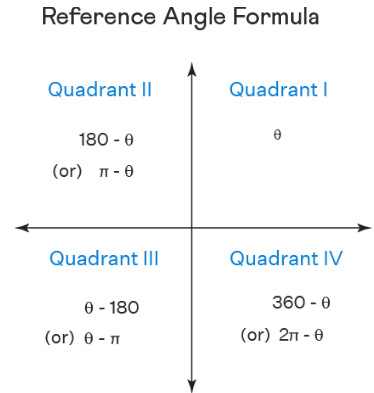
Rules for reference angles in each quadrant

Here are the reference angle formulas depending on the angle quadrant:

Steps to find reference angles

The steps to find the reference angle of an angle are as follows:

1. Find the coterminal angle of the given angle that lies between \(0°\) and \(360°\).
2. If the angle of step \(1\) is between \(0\) and \(90°\), that angle itself is the reference angle of the given angle. If not, then we need to check if it is close to \(180°\) or \(360°\) and how much.
3. The angle from step \(2\) is the angle reference angle.

Reference Angles – Example 1:

Find the reference angle of \(\frac{8π}{3}\) in radians.

Solution:

First, find the coterminal angle. To find its coterminal angle subtract \(2π\) from it.

\(\frac{8π}{3} – 2π = \frac{2π}{3}\)

This angle is not between \(0\) and \(\frac{π}{2}\). Therefore, it is not the reference angle of the given angle. Then check whether \(\frac{2π}{3}\) is close to \(π\) or \(2π\) and by how much.

\(\frac{2π}{3}\) is close to \(π\) by \(π – \frac{2π}{3} = \frac{π}{3}\). Therefore, the reference angle of \(\frac{8π}{3}\) is \(\frac{π}{3}\).

Exercises for Reference Angles

Find the reference angle.

1. \(\color{blue}{\frac{31\pi }{9}}\)
2. \(\color{blue}{-250^{\circ }}\)
3. \(\color{blue}{-\frac{25\pi }{18}}\)

1. \(\color{blue}{\frac{4\pi }{9}}\)
2. \(\color{blue}{70^{\circ }}\)
3. \(\color{blue}{\frac{7\pi }{18}}\)