PSAT Math FREE Sample Practice Questions

The Absolute Best Book to Ace the PSAT Math Test

10 Sample PSAT Math Practice Questions

1- Types of air pollution in \(10\) cities of a country

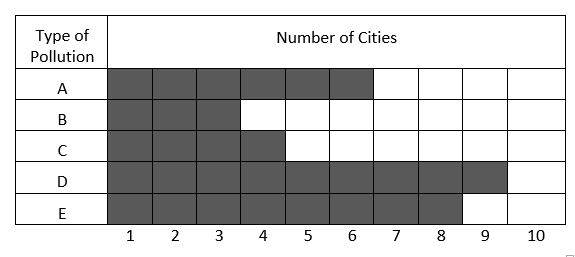
What percent of cities are in the type of pollution \(A, C,\) and \(D\) respectively

A. \(60\%, 40\%, 90\%\)

B. \(30\%, 40\%, 90\%\)

C. \(30\%, 40\%, 60\%\)

D. \(40\%, 60\%, 90\%\)

2- Types of air pollution in \(10\) cities of a country

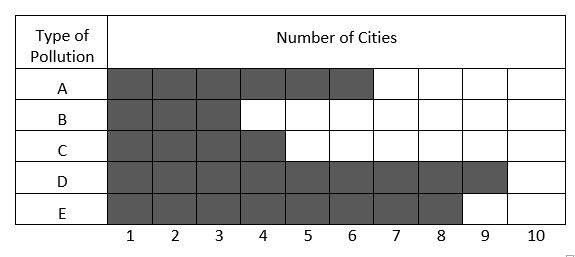
How many cities should be added to the type of pollution \(B\) until the ratio of cities in the type of pollution \(B\) to cities in the type of pollution \(E\) will be \(0.625\)?

A. \(2\)

B. \(3\)

C. \(4\)

D. \(5\)

3- Types of air pollution in \(10\) cities of a country

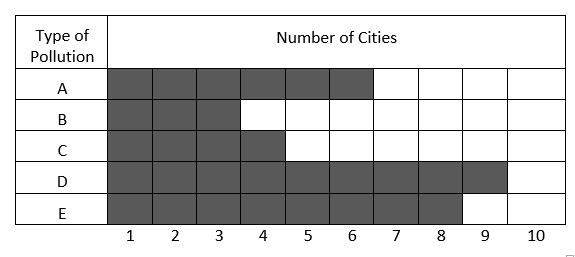
If \(a\) is the mean (average) of the number of cities in each pollution type category, \(b\) is the mode, and \(c\) is the median of the number of cities in each pollution type category, then which of the following must be true?

A. \(a < b< c\)

B. \(b < a < c\)

C. \(a = c\)

D. \(b < c = a\)

4- The ratio of boys and girls in a class is \(4:7\). If there are \(44\) students in the class, how many more boys should be enrolled to make the ratio \(1:1\)?

A. \(8\)

B. \(10\)

C. \(12\)

D. \(16\)

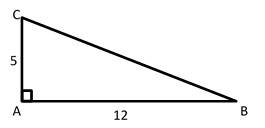
5- In the following right triangle, if the sides AB and AC become twice longer, what will be the ratio of the perimeter of the triangle to its area?

A. \(\frac{1}{2}\)

B. \(2\)

C. \(\frac{1}{3}\)

D. \(3\)

6- The capacity of a red box is \(20\%\) bigger than the capacity of a blue box. If the red box can hold \(30\) equal-sized books, how many of the same books can the blue box hold?

A. \(9\)

B. \(15\)

C. \(21\)

D. \(25\)

7- The sum of six different negative integers is \(-70\). If the smallest of these integers is \( -15\), what is the largest possible value of one of the other five integers?

A. \(-5\)

B. \(-2\)

C. \(-1\)

D. \(0\)

8- What is the ratio of the minimum value to the maximum value of the following function?
\(-2 ≤ x ≤ 3? f(x) = -3x + 1\)

A. \(\frac{7}{8}\)

B. \(-\frac{8}{7}\)

C. \(-\frac{7}{8}\)

D. \(\frac{8}{7}\)

9-

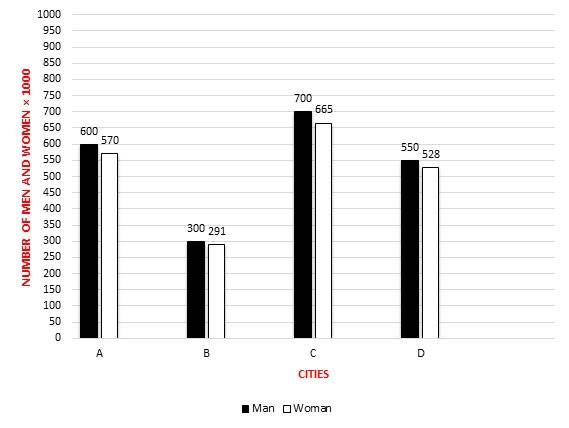
Based on the graph, what’s the maximum ratio of women to men in the four cities?

A. \(0.98\)

B. \(0.97\)

C.\( 0.96\)

D. \(0.95\)

10-

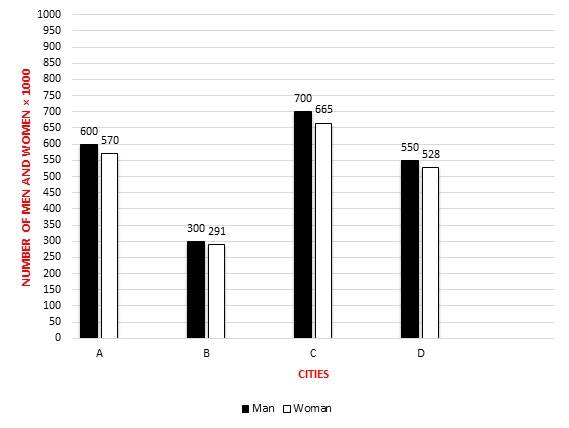
Based on the graph, what’s the ratio of the percentage of men in city \(A\) to the percentage of women in city \(C\)?

A. \(0.9\)

B. \(0.95\)

C. \(1\)

D. \(1.05\)

Best PSAT Math Prep Resource for 2024

Answers:

2- A
Let the number of cities should be added to the type of pollution \(B\) be \(x\). Then:
\(\frac{x+3}{8}=0.625→x+3=8×0.625→x+3=5→x=2\)

3- C
Let’s find the mean (average), mode, and median of the number of cities for each type of pollution.
Number of cities for each type of pollution: \(6, 3, 4, 9, 8\)
\(Mean (Average) = \frac{sum \space of \space terms}{number \space of \space terms}=\frac{6+3+4+9+8}{5}=\frac{30}{5}=6\)
The median is the number in the middle. To find the median, first list numbers in order from smallest to largest.
\(3, 4, 6, 8, 9\)
The median of the data is \(6\).
Mode is the number that appears most often in a set of numbers. Therefore, there is no mode in the set of numbers.
Median = Mean, then, \(a=c\).

4- C
The ratio of boys to girls is \(4:7\). Therefore, there are \(4\) boys out of \(11\) students. To find the answer, first, divide the total number of students by \(11\), then multiply the result by \(4\).
\(44 ÷ 11 = 4 ⇒ 4 × 4 = 16\)
There are \(16\) boys and \(28 (44 – 16)\) girls. So, \(12\) more boys should be enrolled to make the ratio \(1:1\).

5- A
\(AB = 12\) And\( AC = 5\)
\( BC = \sqrt {(12^2+5^2 )}=\sqrt{(144+25)}=\sqrt {169}=13 \)
Perimeter \(= 5 + 12 + 13 = 30\)
\(\frac{5×12}{2}=5×6=30\)
In this case, the ratio of the perimeter of the triangle to its area is: \(\frac{30}{30} = 1\)
If the sides \(AB\) and \(AC\) become twice longer, then:
\( AB=24 \space And \space AC=10\)
\(BC=\sqrt{(24^2+10^2 )}=\sqrt{(576+100)}=\sqrt {676}=26\)
Perimeter\( = 26 + 24 + 10 = 60\)
\(\frac{10×24}{2}=10×12=120\)
In this case, the ratio of the perimeter of the triangle to its area is:
\(\frac{60}{120}=\frac{1}{2}\)

6- D
The capacity of a red box is \(20\%\) bigger than the capacity of a blue box and it can hold \(30\) books. Therefore, we want to find a number that \(20\%\) is bigger than that number is \(30\). Let \(x\) be that number. Then:
\( 1.20 × x = 30\)
Divide both sides of the equation by \(1.2\). Then:
\(x = \frac{30}{1.20}=25\)

7- A
The smallest number is \(-15\). To find the largest possible value of one of the other five integers, we need to choose the smallest possible integers for four of them. Let \(x\) be the largest number. Then:
\(-70 = (-15) + (-14) + (-13) + (-12) + (-11) + x→-70 =- 65 + x
→x = -70 + 65 = -5\)

8- B
Since \(f(x)\) is linear function with a negative slop, then when \(x=-2, f(x)\) is maximum and when \(x=3, f(x)\) is minimum. Then the ratio of the minimum value to the maximum value of the function is:
\(\frac{f(3)}{f(-2)}=\frac{-3(3)+1}{-3(-2)+1}=\frac{- 8}{7}\)

9- B
Ratio of women to men in city A: \(\frac{570}{600}=0.95\)
Ratio of women to men in city B: \(\frac{291}{300}=0.97\)
Ratio of women to men in city C: \(\frac{667}{700}=0.95\)
Ratio of women to men in city D: \(\frac{528}{550} =0.96\)

10- D
Percentage of men in city \(A = \frac{600}{1170}×100 = 51.28 \% \)
Percentage of women in city \(C =
\frac{665}{1365} ×100 = 48.72\%\)
Percentage of men in city \(A\) to percentage of women in city \(C\)
\(\frac{51.28}{48.72} = 1.05\)

College Entrance Tests

The Best Books to Ace the PSAT Math Test