Properties of the Vertical Lines

A vertical line is always a straight line that goes up to down or down to up. Vertical lines are also known as standing lines. The lines that join the bases of a square or rectangle are the vertical lines that we usually draw.

Related Topics

• Properties of the Horizontal Line

A step-by-step guide to properties of the vertical line

A vertical line is a line on the coordinate plane where all the points on the line have the same \(x\)-coordinate. When we draw the points of the function \(x = a\), on a coordinate plane, we find that a vertical line is obtained by joining the coordinates.

In the image below, \(L1\) and \(L2\) are the two vertical lines. All the points in the \(L1\) have only \(a\) as the \(x\)-coordinate for all the values of \(y\), and all the points in the \(L2\) have only \(-a\) as the \(x\)-coordinate for all the values of \(y\).

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

Vertical line equation

The equation of a vertical line is \(x = a\) or \(x = -a\), where \(x\) is the coordinate of \(x\) at any point on the line and \(a\) is where the line crosses the \(x\)-intercept.

The slope of a vertical line

A vertical line has an undefined slope. According to the definition of slope, we calculate the slope as follows:

\(m=\frac {(y_2-y_1)}{(x_2-x_1)}\)

Now, since the \(x\)-coordinate remains constant on a vertical line, therefore we have \(x_2=x_1=x\). So, the slope of the vertical line is \(m=\frac{(y_2-y_1)}{(x-x)}=\frac{(y_2-y_1)}{0}\), which is not defined as the denominator is zero.

The \(x\) coordinates remain the same for all the points on the vertical line and there is no run horizontally. Thus the slope of a vertical line is undefined.

Properties of the vertical line

• The vertical line equation does not have a \(y\)-intercept, because the line is parallel to the \(y\)-axis.
• The equation of a vertical line always takes the form \(x = a\), where a is the \(x\)-intercept.
• The slope of a vertical line is not defined. Since there are no changes in the \(x\) coordinates, the denominator of the slope is zero.

The Ultimate Middle School Math Bundle Grades 6-8

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

Properties of the Vertical Line – Example 1:

What is the slope of the line \(x=-7\)?

Solution:

The slope of a vertical line is undefined. So the slope of the vertical line \(x=-8\) is undefined.

Exercises for Properties of the Vertical Line

• What is the equation of the vertical line passing through \((-11,3)\)?

• Find the equation of the vertical line in the graph.

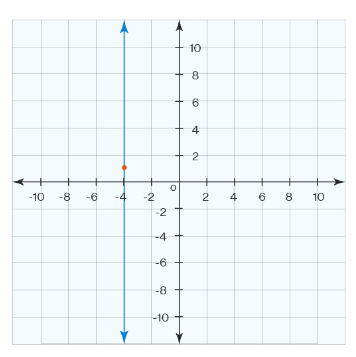
• \(\color{blue}{x+11=0}\)
• \(\color{blue}{x+4=0}\)