How to Find the Central Angle of a Circle?
TL;DR: Picture a pizza, then draw two cuts from the very center out to the crust. The angle those cuts form is a central angle — its vertex sits right at the circle's middle. Here's the handy fact you'll lean on constantly: a central angle's degree measure is exactly equal to the arc it carves out on the crust. To turn that arc measure into actual arc length, take the angle as a fraction of 360 and multiply by the circle's full circumference. One simple proportion, no mystery.
Key takeaways:
- A central angle is formed by two radii of the same circle.
- Central angle measure = intercepted arc measure (in degrees).
- Full circle = \(360^\circ\); semicircle = \(180^\circ\); quarter-circle = \(90^\circ\).
- Arc length: \(s = \dfrac{\theta}{360} \times 2\pi r\), or in radians \(s = r\theta\).
- Sector area: \(A = \dfrac{\theta}{360} \times \pi r^2\).
The central angle is useful for dividing a circle into sections. A slice of pizza is a good example of a central angle. A pie chart consists of several sections and helps to display different values.
A step-by-step guide to finding the central angle of a circle
The central angle is the angle subtended by an arc of a circle at the center of a circle. Radius vectors form the arms of the central angle.
In other words, it is an angle whose vertex is the center of a circle whose arms are two radii lines that intersect at two different points in the circle. When these two points are connected, they form an arc. The central angle is the angle subtended by this arc at the center of the circle.
How to find the central angle of a circle?
The central angle is the angle between the two radii of the circle. To find the central angle, we need to find the length of the arc and the length of the radius. The following steps show how to calculate the central angle in radians.
There are three simple steps to finding the central angle:
- Identify the ends of the arc and the center of the circle (curve). \(AB\) is the arc of the circle and \(O\) is the center of the circle.
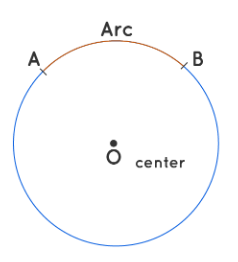
- Connect the end of the arc with the center of the circle. Also, measure the length of the arc and its radius. Here \(AB\) is the arc length and \(OA\) and \(OB\) are the radii of the circle.
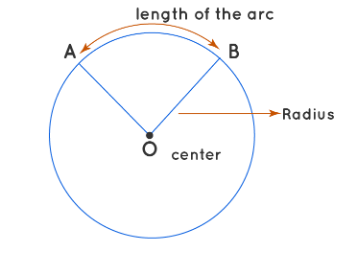
- Divide the length of the curve by the radius to get the central angle. Using the following formula, we will find the value of the central angle in radians.
\(\color{blue}{Central\:Angle=\frac{Length\:of\:the\:Arc}{Radius}}\)
Finding the Central Angle of a Circle – Example 1:
If the arc length is \(8\) inches and the central angle is \(120\) degrees, find the radius of the arc.
Solution:
\(Radius\:of\:the\:arc= 8\space inches\)
\(Central\:angle= 120°\)
\(Central\:angle\:=\frac{\left(length\:of\:arc\:×\:360°\right)}{\left(2\pi \:×\:radius\right)}\)
\(radius\:=\frac{\left(length\:of\:arc\:×360°\right)}{\left(2\pi \:×\:Central\:angle\right)}\)
\(radius\:=\frac{\left(8\:×\:360°\right)}{\left(2\pi \:×120°\right)}\)
\(radius\:=\frac{12}{\pi \:}\)
Exercises for Finding the Central Angle of a Circle
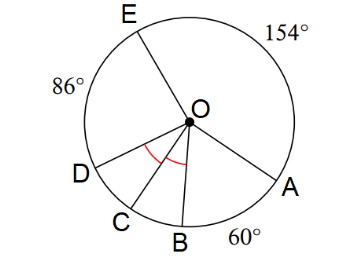
- From the diagram shown, find the \(m∠BOD\) measure.
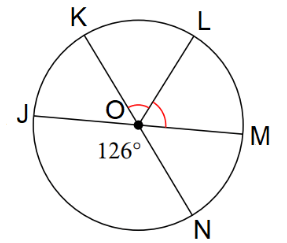
- From the diagram shown, find the \(m∠arc MNK\) measure.
- If the arc length measurement is about \(21\space cm\) and the length of the radius measures \(10\space cm\), find the central angle.
- \(\color{blue}{60°}\)
- \(\color{blue}{234°}\)
- \(\color{blue}{120.38°}\)
Recommended EffortlessMath Books
For a deeper walk through every geometry skill from the ground up, Geometry for Beginners covers angles, area, volume, triangles, and transformations with worked examples and plenty of practice. For algebra-heavy geometry topics, the companion Algebra I for Beginners ties the coordinate-plane work back to linear equations.
Frequently Asked Questions
What’s a central angle?
An angle whose vertex is at the center of a circle, with both sides extending out to the circle as radii. The two radii cut off an arc on the circle – the arc that the central angle “intercepts.” A full circle has \(360^\circ\) of central angles around the center.
What’s the relationship between a central angle and its arc?
The central angle’s measure (in degrees) equals the arc’s measure (also in degrees). A \(45^\circ\) central angle cuts a \(45^\circ\) arc; a \(120^\circ\) central angle cuts a \(120^\circ\) arc. They’re the same number – that’s the central angle theorem in its simplest form.
How is arc measure different from arc length?
Arc measure is in degrees and matches the central angle. Arc length is the actual distance along the curve, in units of length (cm, inches, etc.). Two circles can have the same arc measure (\(60^\circ\)) but very different arc lengths if their radii differ.
What’s the formula for arc length?
\(s = \dfrac{\theta}{360} \times 2\pi r\), with \(\theta\) in degrees and \(r\) the radius. The fraction \(\dfrac{\theta}{360}\) tells you what portion of the full circumference \(2\pi r\) the arc covers. In radians, the formula simplifies to \(s = r\theta\). Both forms give the actual length traveled along the curve, in the same length units as the radius.
What’s a sector and how do I find its area?
A sector is the pie-slice region between two radii and the arc they cut off. Sector area: \(A = \dfrac{\theta}{360} \times \pi r^2\) (in degrees) or \(A = \dfrac{1}{2}r^2\theta\) (in radians). For a circle of radius 6 and central angle \(90^\circ\): \(A = \dfrac{90}{360} \times \pi(36) = 9\pi \approx 28.27\) square units.
What’s the difference between a central angle and an inscribed angle?
A central angle has its vertex at the center; an inscribed angle has its vertex on the circle’s edge. The inscribed angle theorem says: an inscribed angle is HALF the central angle that intercepts the same arc. So if a central angle is \(80^\circ\), an inscribed angle on the same arc is \(40^\circ\).
How do I convert between degrees and radians?
\(180^\circ = \pi\) radians, so \(1^\circ = \dfrac{\pi}{180}\) radians and \(1\) rad \(= \dfrac{180}{\pi}\) degrees. Multiply degrees by \(\dfrac{\pi}{180}\) to get radians; multiply radians by \(\dfrac{180}{\pi}\) to get degrees. \(90^\circ = \dfrac{\pi}{2}\) rad; \(60^\circ = \dfrac{\pi}{3}\) rad; \(45^\circ = \dfrac{\pi}{4}\) rad.
Walk me through a complete example.
Circle has radius 12 cm and central angle \(45^\circ\). Arc length: \(s = \dfrac{45}{360} \times 2\pi(12) = \dfrac{1}{8} \times 24\pi = 3\pi \approx 9.42\) cm. Sector area: \(A = \dfrac{45}{360} \times \pi(12)^2 = \dfrac{1}{8} \times 144\pi = 18\pi \approx 56.55\) square cm.
What’s an example with pie-chart percentages?
If a pie chart shows that 25% of the data falls in one category, the central angle for that slice is \(0.25 \times 360^\circ = 90^\circ\). To go the other way, divide the central angle by \(360\): a slice with central angle \(60^\circ\) represents \(60/360 = \dfrac{1}{6} \approx 16.7\%\) of the data.
Where does this skill show up?
High school geometry, trigonometry, pre-calculus, and SAT/ACT geometry sections. Real-life uses: pie charts, sector calculations in engineering, satellite coverage areas, irrigation patterns, anything involving fractions of a full rotation. Once you have the central-angle-to-arc relationship, every circle problem opens up.
Related EffortlessMath Lessons
If a topic on this page feels rusty, these short lessons go deeper:
Related to This Article
More math articles
- 5th Grade MEAP Math FREE Sample Practice Questions
- The Best Grade 5 Math Book for Vermont Students
- Full-Length CLEP College Algebra Practice Test
- The Best Algebra 1 Book for Rhode Island Students
- Kelly Criterion for Casino Games: When Math Tells You to Sit Out
- New Mexico MSSA Grade 7 Math Worksheets: 95 Free Printable PDFs with Step-by-Step Keys
- Long Division: How to Deconstruct complex Integrals
- How to Fall in Love with Math and Studying?
- The Ultimate 6th Grade AzMERIT Math Course (+FREE Worksheets)
- Massachusetts Algebra 1 Free Worksheets: Printable Algebra 1 PDF Practice with Student-Friendly Keys
What people say about "How to Find the Central Angle of a Circle? - Effortless Math"?
No one replied yet.