Properties of the Horizontal Line

A straight line that has an intercept only on the \(y\)-axis, not on the \(x\)-axis is called a horizontal line. The base that we draw for flat shapes is a horizontal line.

Related Topics

• Properties of the Vertical Lines

A step-by-step guide to properties of the horizontal line 

Horizontal lines are also known as sleeping lines. In coordinate geometry, horizontal lines are lines that are parallel to the \(x\)-axis. In geometry, we can find horizontal line segments in various shapes such as quadrilaterals, \(3\)D, and so on.

The slope of the horizontal line

The slope of a horizontal line is zero. While calculating \(slope=\frac{rise}{run}\), we see that there is no increases in the \(y\) coordinates because they are the same across the horizontal line. So there are no changes in the \(y\) coordinate and finally, the slope of the horizontal line is \(0\).

Horizontal line equation

According to the previous image, we see that the \(y\) coordinates of all points on a horizontal line are the same. Thus, the equation of a horizontal line through any point \((a,b)\) is of the form: \(y = b\), where \(b\) is constant.

Here \(x\) is absent. It means that the \(x\)-coordinate can be anything whereas the \(y\)-coordinate of all the points on the line must be \(b\) only. The \(y\)-intercept of the horizontal line is \((0, b)\).

Horizontal line test

Horizontal line testing is used to determine whether a function is a one-to-one function. According to the horizontal line test, if there is a horizontal line that passes through more than one point of the graph (function), it is NOT a one-to-one function. In other words, in a one-to-one function, there is only one unique \(x\) value for each \(y\) value.

Drawing horizontal lines

• To draw a horizontal line, we need to know the dimensions of the point (i.e.,\(x\) and \(y\) value).
• Now, we can locate the point in the \(xy\) plane.
• Taking the point \((x,y)\) as the reference point, we need to draw a line parallel to the \(x\)-axis.
• Thus, a horizontal line is drawn.

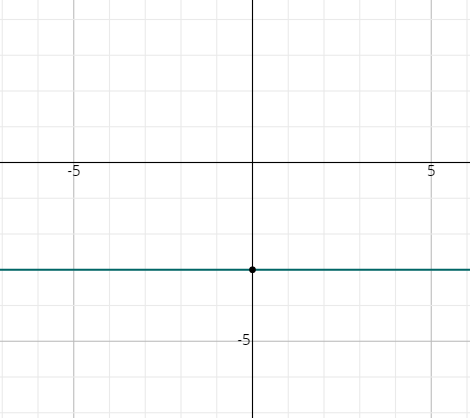
Properties of the Horizontal Line – Example 1:

Draw the horizontal line \(y = -3\).

Exercises for Properties of the Horizontal Line

1. Find the equation of the horizontal line passing through the point \((3,8)\).
2. Determine the horizontal line equation, whose \(y\)-intercept is \((0, 2)\).
3. If a horizontal line passes through the point \((1,-5)\), what is the equation of the line?

1. \(\color{blue}{y=8}\)
2. \(\color{blue}{y=2}\)
3. \(\color{blue}{y=-5}\)