6th Grade MEAP Math Practice Test Questions
The most important factor in strengthening a 6th Grade student’s math skills in the MEAP Math test is enough practice. Using the sample of 6th Grade MEAP Math question is one of the useful tools of practice. Your student can acquire the necessary skills to participate in the 6th Grade MEAP Math test by taking and solving practice test questions. Therefore, in this article, we intend to provide you with the 10 most common 6th Grade MEAP Math practice test questions along with their step-by-step solutions to give your student more control over the test content.
The Absolute Best Book to Ace 6th Grade MEAP Math Test
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
10 Sample 6th Grade MEAP Math Practice Questions
1- What is the missing prime factor of number 420?
\(420=2^2×3^1×…\)
A. \(2^2×3^1×5^1×7^1\)
B. \(2^2×3^1×7^1×9^1\)
C. \(1^2×2^3×2^1×3^1\)
D. \(3^2×5^1×7^1×9^1\)
2- If the area of the following trapezoid is equal to \(A\), which equation represents \(x\)?
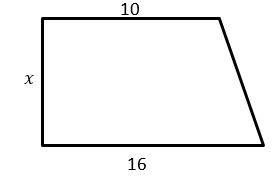
A. \( x = \frac{13}{A}\)
B. \( x = \frac{A}{13}\)
C. \( x=A+13\)
D. \( x=A-13\)
3- By what factor did the number below change from the first to the fourth number?
\(8, 104, 1352, 17576\)
A. 13
B. 96
C. 1456
D. 17568
4- 170 is equal to …
A. \( -20-(3×10)+(6×40)\)
B. \(((\frac{15}{8})×72 )+ (\frac{125}{5}) \)
C. \(((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4}\)
D. \(\frac{481}{6} + \frac{121}{3}+50\)
5- The distance between the two cities is 3,768 feet. What is the distance between the two cities in yards?
A. 1,256 yd
B. 11,304 yd
C. 45,216 yd
D. 3,768 yd
6- Mr. Jones saves $3,400 out of his monthly family income of $74,800. What fractional part of his income does Mr. Jones save?
A. \(\frac{1}{22}\)
B. \(\frac{1}{11}\)
C. \(\frac{3}{25}\)
D. \(\frac{2}{15}\)
7- What is the lowest common multiple of 12 and 20?
A. 60
B. 40
C. 20
D. 12
8- Based on the table below, which expression represents any value of f in term of its corresponding value of \(x\)?
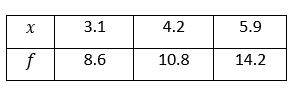
A. \(f=2x-\frac{3}{10}\)
B. \(f=x+\frac{3}{10}\)
C. \(f=2x+2 \frac{2}{5}\)
D. \(2x+\frac{3}{10}\)
9- 96 kg \(=\)… ?
A. 96 mg
B. 9,600 mg
C. 960,000 mg
D. 96,000,000 mg
10- Calculate the approximate area of the following circle? (the diameter is 25)
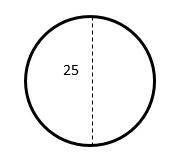
A. 78
B. 491
C. 157
D. 1963
Best 6th Grade MEAP Math Prep Resource for 2022
Answers:
1- A
\(420=2^2×3^1×5^1×7^1\)
2- B
The area of the trapezoid is: area= \(\frac{(base 1+base 2)}{2})×height= ((\frac{10 + 16}{2})x = A\)
\( →13x = A→x = \frac{A}{13}\)
3- A
\(\frac{104}{8}=13, \frac{1352}{104}=13, \frac{17576}{1352}=13\)
Therefore, the factor is 13
4- C
Simplify each option provided.
\( A. -20-(3×10)+(6×40)=-20-30+240=190\)
\( B. (\frac{15}{8})×72 + (\frac{125}{5}) =135+25=160\)
\(C. ((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4} = ((\frac{30 + 30}{4})×8)- \frac{11}{2}+ \frac{111}{2}=(\frac{60}{4})×8) + \frac{100}{2}= 120 + 50 = 170\)this is the answer
\(D. \frac{481}{6} + \frac{121}{3}+50= \frac{481+242}{6}+50=120.5+50=170.5\)
5- A
1 yard \(= \)3 feet
Therefore, \(3,768 ft × \frac{1 \space yd }{3 \space ft}=1,256 \space yd\)
6- A
3,400 out of 74,800 equals to \(\frac{3,400}{74,800}=\frac{17}{374}=\frac{1}{22}\)
7- A
Prime factorizing of \(20=2×2×5\)
Prime factorizing of \(12=2×2×3\)
LCM\(=2×2×3×5=60\)
8- C
Plug in the value of \(x\) into the function f. First, plug in 3.1 for \(x\).
\(A. f=2x-\frac{3}{10}=2(3.1)-\frac{3}{10}=5.9≠8.6\)
\(B. f=x+\frac{3}{10}=3.1+\frac{3}{10}=3.4≠10.8\)
\(C. f=2x+2 \frac{2}{5}=2(3.1)+2 \frac{2}{5}=6.2+2.4=8.6 \)
This is correct!
Plug in other values of \(x. x=4.2\)
\(f=2x+2\frac{2}{5} =2(4.2)+2.4=10.8 \)
This one is also correct.
\(x=5.9\)
\(f=2x+2 \frac{2}{5}=2(5.9)+2.4=14.2 \)
This one works too!
\(D. 2x+\frac{3}{10}=2(3.1)+\frac{3}{10}=6.5≠8.6\)
9- D
1 kg\(=\) 1000 g and 1 g \(=\) 1000 mg
96 kg\(=\) 96 \(×\) 1000 g \(=\)96 \(×\) 1000 \(×\) 1000 \(=\)96,000,000 mg
10- B
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{25}{2}\).
Area of a circle = \(πr^2=π(\frac{25}{2})^2=156.25π=156.25×3.14=490.625≅491\)
Looking for the best resource to help you succeed on the MEAP Math Grade 6 Math test?
The Best Books to Ace 6th Grade MEAP Math Test
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- Volume of Cubes
- How to Use Number Lines for Multiplication by a Negative Integer?
- Top 10 Tips to Overcome TSI Math Anxiety
- How to Find Data Distribution
- Top 10 Tips to Create a CHSPE Math Study Plan
- The Ultimate Praxis Core Math Course (+FREE Worksheets & Tests)
- How to Solve Logarithmic Equations? (+FREE Worksheet!)
- Top 10 8th Grade PSSA Math Practice Questions
- The Ultimate 6th Grade GMAS Math Course (+FREE Worksheets)
- Fine-Tuning Division: The Art of Adjusting Quotients
What people say about "6th Grade MEAP Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.