How to Understand the Real Number Line

Step-by-step Guide to Understand the Real Number Line

Here is a step-by-step guide to understand the real number line:

Step 1: Distinction Between Rational and Irrational Numbers

• Rational Numbers (Q): These can be expressed as the quotient or fraction \(\frac{p}{q}\)​ of two integers, where \(p\) (numerator) and \(q\) (denominator) are integers and \(q≠0\). Examples include \(\frac{1}{2}, 5, -3\), etc.
• Irrational Numbers: Numbers that can’t be written as simple fractions or ratios. This set includes numbers like \(π\) and \(\sqrt{2}\)​, which don’t terminate or repeat in their decimal form.

Step 2: Bridging The Gap – The Union

The real numbers encompass both rational and irrational numbers. Hence, the set of real numbers (\(R\)) is a harmonious blend, or union, of these two sets.

Step 3: Visualizing the Infinite: The Real Number Line

Imagine an infinitely stretching line. At one distinct point, it houses the number \(0\). Moving to the right, the numbers increase, and to the left, they decrease. This infinite line, punctuated by every conceivable real number, is the Real Number Line. Every point on this line corresponds to a unique real number.

Step 4: Diving Deeper: Intervals and Bounds

• Open Intervals: Represented as \((a, b)\), it includes all numbers between \(a\) and \(b\) but not the endpoints themselves.
• Closed Intervals: \([a, b]\) includes all the numbers between and including \(a\) and \(b\).
• Infinite Intervals: These can be open or closed on one side and stretch infinitely on the other, like \([a, ∞)\) or \((-∞, b]\).

Step 5: Density Property

In the intricate tapestry of the real number line, between any two distinct real numbers, no matter how close, there exists another real number. This speaks to the unfathomable density and continuity of real numbers on this line.

Step 6: Beyond the Real – A Glimpse

Real numbers have their limitations. They don’t cater to the square root of negative numbers, leading us to another domain – the complex numbers. But that’s a story for another day.

Step 7: Conclusion

The Real Number Line is not just a representation; it’s an embodiment of the ceaseless continuum of numbers that mold our mathematical and physical reality. Through it, we can visualize, compare, and better grasp the realm of real numbers, from the utterly rational to the bafflingly irrational.

In immersing ourselves in the tapestry of the real number line, we not only understand numbers better but also develop an appreciation for the infinite expanse and potential of mathematics.

Examples:

Example 1:

Locate \(\frac{3}{4}\) on the number line.

Solution:

Consider the number \(\frac{3}{4}\)​ (or \(0.75\) in decimal form). This is a rational number, and on the real number line, it would be located three-fourths of the way from \(0\) to \(1\).

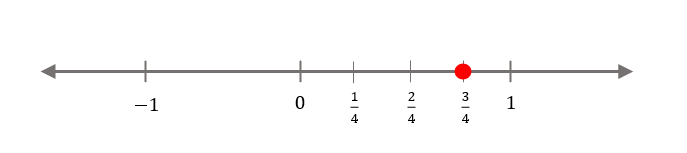
Example 2:

Locate \(−2.5\)​ on the number line.

Solution:

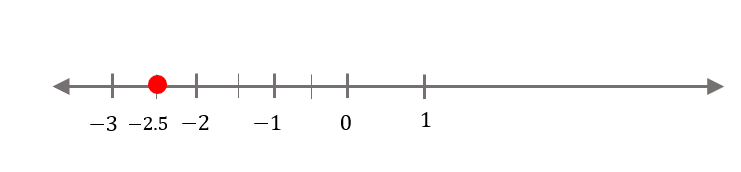
Consider the number \(−2.5\). This is a rational number, and on the real number line, it would be located to the left of \(0\) and halfway between \(-2\) and \(-3\).