How to Scale a Function Vertically?
Scaling is a process of changing the size and shape of the graph of the function. In this blog post, you will learn how to vertical scaling.

Vertical scaling refers to the shrinking or stretching of the curve along the \(y\)-axis by some specific units.
Related Topics
A step-by-step guide to vertical scaling
There are four types of transformation possible for a graph of a function, which are:
- Rotations
- Translations
- Reflections
- Scaling
In addition, scaling can be divided into two different types, e.g.
- Horizontal scaling
- Vertical scaling
Vertical scaling refers to changing the shape and size of a function graph along the \(y\)-axis and is done by multiplying the function by a fixed value.
The shape of the curve depends on the value of \(C\):
- If \(C > 1\), the graph stretches and makes the graph steeper.
- If \(C < 1\), the graph shrinks and makes the graph flatter.
How to do vertical scaling?
Let’s understand this with an example:
Suppose we have a basic quadratic equation \(f(x)=x^2\) and a graphical representation of the diagram is shown below.
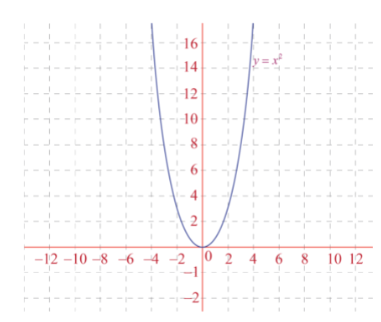
If we want to vertically scale this chart, we have to follow the given steps:
Step 1: Select the constant with which we want to scale the function.
Here we have selected \(+2\).
Step 2: Write the new function as \(g(x)=C f(x)\), where \(C\) is the constant.
Here, the new function will be: \(g(x)=2 f(x)= 2 x^2\)
Step 3: Trace the new function graph by replacing each value of \(y\) with \(Cy\).
Here we need to replace the value of the \(y\)-coordinate by \(2y\).
The \(Y\) coordinates of each point in the graph are multiplied by \(±C\), and the curve shrinks or stretches accordingly.
Here we have the graph \(x\) and it is stretched in the \(y\)-direction with a factor of \(+2\).
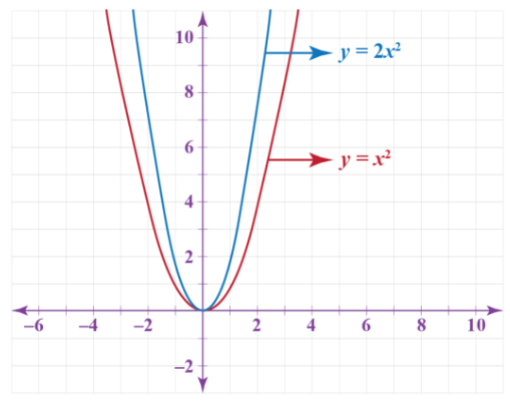
Note: As we have scaled it with a factor of \(+2\) units, it has made the graph steeper.
Vertical Scaling – Example 1:
Vertically stretch the function \(y=(x+2)\) by a factor of two.
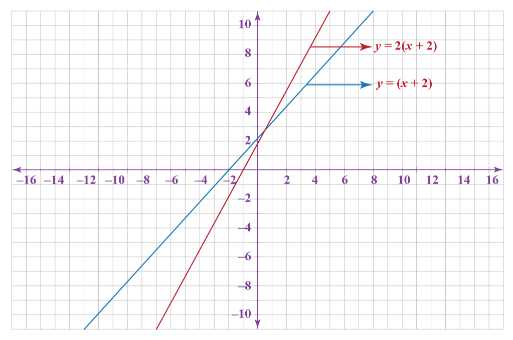
Exercises for Vertical Scaling
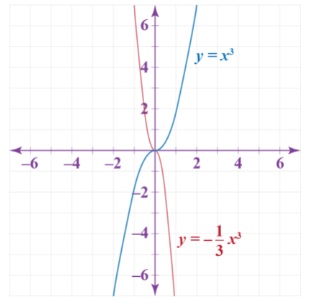
- Vertically stretch the function \(f(x)=x^3\) by a factor of \(-\frac{1}{3}\).


Related to This Article
More math articles
- SAT versus PSAT: What You Need to Know
- The Ultimate NYSTCE Grades 1-6 Math (222) Course (+FREE Worksheets & Tests)
- 5th Grade FSA Math Practice Test Questions
- 6th Grade MAP Math Worksheets: FREE & Printable
- Full-Length 7th Grade STAAR Math Practice Test
- 5th Grade ACT Aspire Math Worksheets: FREE & Printable
- How to Modeling Real-World Situations Using Functions
- How to Prepare for the CBEST Math Test?
- How to Graph Absolute Value Function?
- Math As The Language Of Chance: An Introduction To Probability


























What people say about "How to Scale a Function Vertically? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.