How to Model and Solve Equations Using Algebra Tiles

A Step-by-step Guide to Modeling and Solving Equations Using Algebra Tiles

Here are the basic steps to follow:

Step 1: Understanding the Algebra Tiles

Algebra tiles are physical or digital manipulatives used to represent algebraic expressions. There are typically three types:

1. A small square to represent the number \(1\). These tiles often come in two colors to differentiate between positive (usually represented by yellow) and negative values (usually represented by red).
2. A rectangular tile that represents the variable “\(x\)”. Like the square tile, these often come in two colors to distinguish between positive and negative.
3. A larger square tile to represent “\(x^2\)”. These also come in two colors for positive and negative values.

Step 2: Setting Up the Equation

Let’s consider an example equation: \(3x + 2 = x + 4\)

On the left side of the equation, you would place \(3\) ‘\(x\)’ tiles and \(2\) unit tiles. On the right side of the equation, place \(1\) ‘\(x\)’ tile and \(4\) unit tiles. Your setup represents the equation visually.

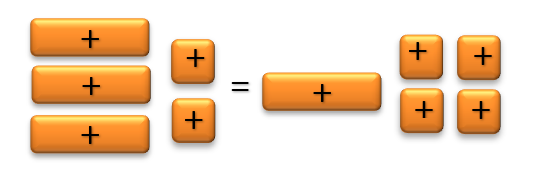
Step 3: Simplifying the Equation

The goal is to isolate ‘\(x\)’ on one side of the equation. To do this, you can “remove” tiles from both sides to maintain balance. In this context, “removing” a tile means pairing a positive tile with a negative tile which results in a zero pair, effectively eliminating them.

Following our example:

• Subtract \(1\) ‘\(x\)’ tile from both sides. This leaves us with \(2x + 2 = 4\).
• Now subtract \(2\) unit tiles from both sides. This gives us the equation \(2x = 2\).

Now, we have two ‘\(x\)’ tiles equal to two ‘\(1\)’ tiles. This implies that each ‘\(x\)’ tile is equivalent to one ‘\(1\)’ tile.

Step 4: Determining the Solution

Since each ‘\(x\)’ tile equates to one ‘\(1\)’ tile, it’s clear that the solution to our equation is \(x = 1\).

Step 5: Checking the Solution

Check the solution by substituting the value of ‘\(x\)’ back into the original equation. In this case, substitute \(x\) with \(1\) in the equation \(3x + 2 = x + 4\). You should find that both sides of the equation balance, confirming the solution is correct.

Using algebra tiles can provide a tangible, visual way to solve equations, making it easier to understand the principles of algebra. While this method is beneficial for beginners and less complex equations, it may not be the most efficient for more complicated algebraic equations.