How to Graphs of Rational Functions?

The rational function is defined as a polynomial coefficient whose denominator has a degree of at least \(1\). In other words, there must be a variable in the denominator.

The general form of a rational function is \(\frac{p(x)}{q(x)}\). where \(p(x)\) and \(q(x)\) are polynomials and \(q(x)≠0\).

Related Topics

• How to Add and Subtract Rational Expressions
• How to Multiply Rational Expressions
• How to Solve Rational Equations

A step-by-step guide to graphs of rational functions

It can be challenging to draw graphs of rational functions. Finding the asymptotes and intercepts is a fine place to begin when attempting to graph a rational function.

Graphing rational functions involves a series of steps:

• Determine if the rational function has any asymptotes
• Asymptotes should be drawn as dotted lines.
• Find the rational function’s \(x\) and \(y\)-intercepts, if any.
• Determine the \(y\) values for a variety of \(x\) values.
• Draw a smooth curve connecting the points by plotting them on a graph. Don’t cross-vertical asymptotes.

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.

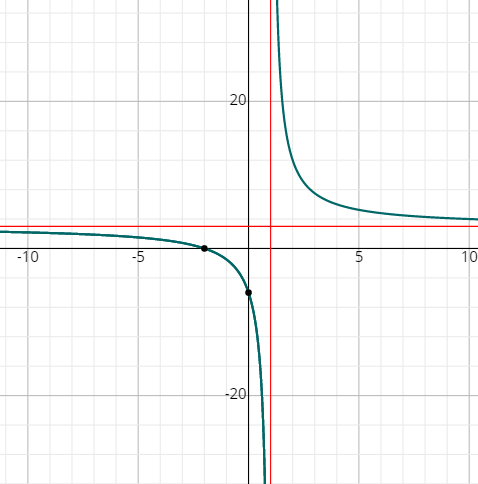
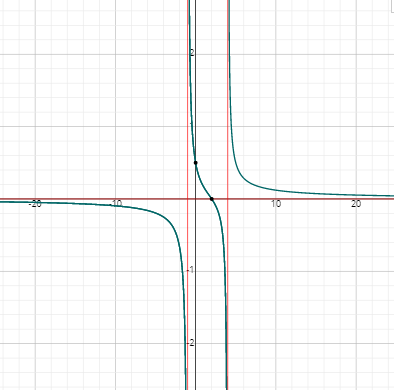
Graphs of Rational Functions – Example 1:

Draw a graph of the following function. \(f(x)=\frac{3x+6}{x-1}\)

First, we need to determine the vertical asymptotes:

\(x-1=0 → x=1 \)

And the horizontal asymptote is:

\(y=\frac{3}{1}=3\)

Then, the \(x\)-intercepts will be,

\(3x+6=0 → 3x=-6 → x=-\frac{6}{3}=-2\), the \(x\)-intercepts is \((-2,0)\)

The \(y\)-intercept is:

\(f(0)=\frac{3(0)+6}{0-1}\) → \(f(0)=\frac{6}{-1}=-6\), the \(y\)-intercepts is \((0,-6)\)

We need to find more points on the function and graph the function.

Now, putting all this together gives the following graph.

Exercises for Graphs of Rational Functions

Draw a graph of the following function.

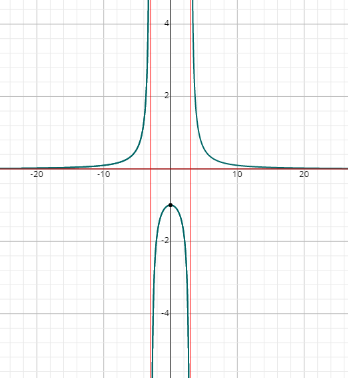
• \(\color{blue}{f(x)=\frac{9}{x^2-9}}\)

• \(\color{blue}{f(x)=\frac{4x^2+x}{2x^2+x}}\)

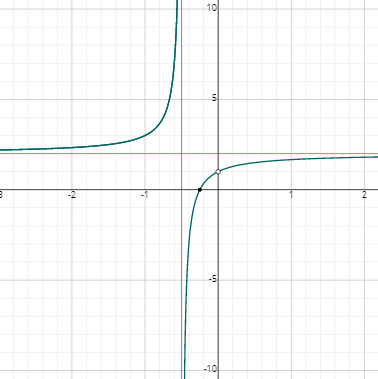
• \(\color{blue}{f(x)=\frac{x-2}{x^2-3x-4}}\)

\(\color{blue}{f(x)=\frac{9}{x^2-9}}\)

\(\color{blue}{f(x)=\frac{4x^2+x}{2x^2+x}}\)

\(\color{blue}{f(x)=\frac{x-2}{x^2-3x-4}}\)

The Ultimate Middle School Math Bundle Grades 6-8

Download

$109.99 Original price was: $109.99.$54.99Current price is: $54.99.