How to Find Slope From a Graph?

The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of a line in the coordinate plane. In general, to find the slope of a line, we must have values of both different coordinates on the line.

Related Topics

• How to Find Slope

A step-by-step guide to finding slope from a graph

The process of finding the slope from a graph uses the slope formula \(\frac{rise}{run}\). When the graph of a line is given and we are asked to find its equation, the first thing that we need to do is to find its slope.

Finding slope from a graph

The slope of a line is the ratio of increase to execution. Hence, here are the steps to find the slope of the chart:

• Step 1: Select any two random points on the graph of the line (preferably with integer coordinates).
• Step 2: Label them as \(A\) and \(B\) (in any order).
• Step 3: Calculate “rise” from \(A\) to \(B\). As we go from \(A\) to \(B\) vertically, if we have to go “up”, then the rise is positive; “down”, then the rise is negative.
• Step 4: Now, use the formula: \(\color{blue}{slope =\frac{rise}{run}}\).

Calculating slope from a graph using the slope formula

The slope formula is used to find the slope of a line that joins two points \((x_1, y_1)\) and \((x_2, y_2)\). sing this formula, the slope of the line is, \(\color{blue}{m = \frac{(y_2 – y_1)}{ (x_2 – x_1)}}\). We can use the same formula to find the slope of a line from its graph also. For this:

• Step 1: Select both points on the line from its graph.
• Step 2: Represent them as \((x_1, y_1)\) and \((x_2, y_2)\) in any order.
• Step 3: Apply the formula \(m = \frac{(y_2 – y_1)}{ (x_2 – x_1)}\) to find the slope.

Exercises for Finding Slope From a Graph

Find the slope of the line from the following graphs using the \(\frac{rise}{run}\) formula.

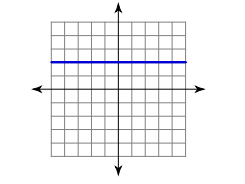
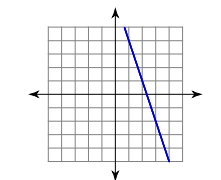
1. \(\color{blue}{0}\)
2. \(\color{blue}{-3}\)