How to Find Elapsed Time?

We can define time as the period during which a particular event occurs, has occurred, or is about to occur. It is a measurable quantity and also infinite.

Related Topics

• Measurements – Time

A step-by-step guide to finding elapsed time

Adding time in mathematics is a process that is done by adding distinct units of time such as hours, minutes, and seconds and then integrating them. The normal addition has a unit broken into \(1, 10, 100\), etc subunits, and in time the unit of time is broken into \(60\) subunits. This distinction sometimes makes it a little difficult to add time. The following table shows the unit values of the time.

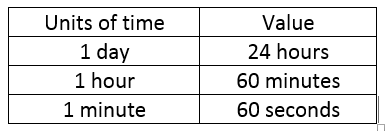
Subtracting time

Subtraction of time is approximately equal to addition time. To do this, we follow some simple steps.  First, subtract the hours, and then subtract the minutes. In addition, write the resultant answer of hours and minutes.

For example, subtract \(6:45\) from \(8:55\). First, let’s reduce the hours by \(8-6 = 2\), then we can subtract the minutes by \(55- 45 = 10\). The result can be written together as \(2:10\).

Adding hours and minutes

If we know the conversion time, it is very easy to add time in hours and minutes.  First, add all the hours of the two times. Now add the minutes of the two given times. Write the time obtained in hours: minutes format.

For example, let’s add a set of two times, \(9:10\) and \(1:15\). The sum of \(9\) and \(1\) o’clock is equal to \(10\). Adding \(10\) and \(15\) minutes equals \(25\). Then we write the calculated hour and minute together at \(10:25\).

Notes:

• Add all hours and minutes to calculate the total time. Similarly, subtract all the hours and minutes to calculate the time.
• When adding minutes, if it exceeds \(60\), delete \(60\) and count the remaining minutes as a total. Deleted \(60\) minutes are converted to an hour and added to the hour.
• When subtracting minutes, if minutes are negative, then add \(60\) minutes with them and consider their total as minutes. The added \(60\) minutes, which in turn is considered one hour, is removed from the total hour.

Finding Elapsed Time – Example 1:

John plans to go to a park. He takes a taxi at \(3.45\space pm\). It takes about \(1\) hour and \(5\) minutes to reach the destination. What time does John get to the park?

Solution:

The initial time is \(3.45\space pm\). And the travel time is \(1\) hour and \(5\) minutes. By adding the hours we have, \(3 + 1 = 4\) hours, and by adding the minutes, we will have \(45 + 5 = 50\) minutes. Therefore John reaches the park at \(4:50\space pm\).

Exercises for Finding Elapsed Time

1. Anna arrived at school at \(7:59\space a.m.\) and left school at \(2:33\space p.m\). How long was Anna at school?
2. Jaydon started his homework at \(6:30\space pm\) and finished it at \(8\space pm\). How many hours and minutes did Jaydon spend completing his homework?
3. Brandon got to work at \(8:10\space a.m\). and left at \(3:45\space p.m\). How long did Brandon work?
4. Caleb ran a marathon in \(2\) hours and \(17\) minutes. He crossed the finish line at \(10:33\) in the morning, what time did the race start?

1. \(\color{blue}{6\:hours\:and\:34\:minutes}\)
2. \(\color{blue}{1\:hour\:and\:30\:minutes}\)
3. \(\color{blue}{7\:hours\:and\:35\:minutes}\)
4. \(\color{blue}{8:16\:a.m}\)